
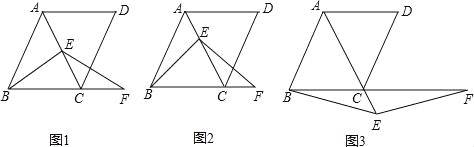
【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
(1)如图1,当E是线段AC的中点,且AB=2时,求△ABC的面积;
(2)如图2,当点E不是线段AC的中点时,求证:BE=EF;
(3)如图3,当点E是线段AC延长线上的任意一点时,(2)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
【答案】(1) ![]() ;(2)证明见解析;(3)见解析
;(2)证明见解析;(3)见解析
【解析】
试题分析:(1)根据菱形的性质证明△ABC是等边三角形和AB=2,求出△ABC的面积;
(2)作EG∥BC交AB于G,证明△BGE≌△ECF,得到BE=EF;
(3)作EH∥BC交AB的延长线于H,证明△BHE≌△ECF,得到BE=EF.
试题解析:(1)∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC是等边三角形,又E是线段AC的中点,
∴BE⊥AC,AE=![]() AB=1,
AB=1,
∴BE=![]() ,
,
∴△ABC的面积=![]() ×AC×BE=
×AC×BE=![]() ;
;
(2)如图2,作EG∥BC交AB于G,
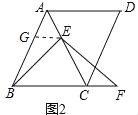
∵△ABC是等边三角形,
∴△AGE是等边三角形,
∴BG=CE,
∵EG∥BC,∠ABC=60°,
∴∠BGE=120°,
∵∠ACB=60°,
∴∠ECF=120°,
∴∠BGE=∠ECF,
在△BGE和△ECF中,
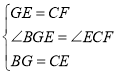 ,
,
∴△BGE≌△ECF,
∴EB=EF;
(3)成立,
如图3,作EH∥BC交AB的延长线于H,
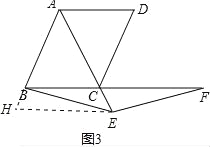
∵△ABC是等边三角形,
∴△AHE是等边三角形,
∴BH=CE,
在△BHE和△ECF中,
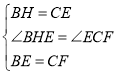 ,
,
∴△BHE≌△ECF,
∴EB=EF.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.形状相同的两个三角形一定全等
B.面积相等的两个三角形一定全等
C.所有的正方形都全等
D.一个图形经过平移后,前后两个图形一定全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程4+2x2﹣5x=0的二次项系数、一次项系数及常数项分别是( )
A. 4,2,5 B. 4,2,﹣5 C. 2.﹣5,4 D. 2,4,﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若多项式3x2-2xy-y2减去多项式M所得的差是-5x2+xy-2y2,则多项式M是( )
A. -2x2-xy-3y2 B. 2x2+xy+3y2 C. 8x2-3xy+y2 D. -8x2+3xy-y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为MN(点M、N分别在边AC、BC上).给出以下判断:
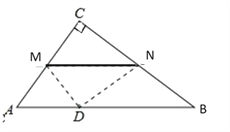
①当MN∥AB时,CM=AM;
②当四边形CMDN为矩形时,AC=BC;
③当点D为AB的中点时,∠CMN=∠B;
④当∠CMN=∠B时,点D为AB的中点;
其中正确的是__.(把所有正确结论序号都填在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三角形的两边长分别为5和3,第三边的边长是方程(x-2)(x-4)=0的根,则这个三角形的面积是( )
A. 6 B. 3
C. 4 D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com