
【题目】在Rt△ABC中,∠ACB=90°,tan∠BAC=![]() . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
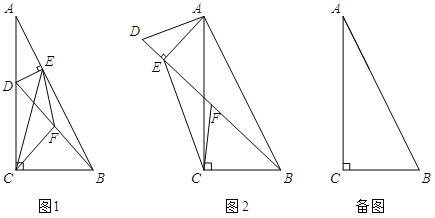
(1)若过点D作DE⊥AB于E,连结CF、EF、CE,如图1.设![]() ,则k= ;
,则k= ;
(2)若将图1中的△ADE绕点A旋转,使得D、E、B三点共线,点F仍为BD中点,如图2所示.求证:BE-DE=2CF;
(3)若BC=6,点D在边AC的三等分点处,将线段AD绕点A旋转,点F始终为BD中点,求线段CF长度的最大值.
【答案】(1)k=1(2)证明![]() ,则可得
,则可得![]() . (3)当点D在靠近点C的
. (3)当点D在靠近点C的
三等分点时,线段CF的长度取得最大值为![]()
【解析】试题分析:解:(1)k=1; .
(2)如图2,过点C作CE的垂线交BD于点G,设BD与AC的交点为Q.

由题意,tan∠BAC=![]() ,
,
∴![]() .
.
∵D、E、B三点共线,
∴AE⊥DB.
∵∠BQC=∠AQD,∠ACB=90°,
∴∠QBC=∠EAQ.
∵∠ECA+∠ACG=90°,∠BCG+∠ACG=90°,
∴∠ECA=∠BCG.
∴![]() .
.
∴![]() .
.
∴GB=DE.
∵F是BD中点,
∴F是EG中点.
在![]() 中,
中, ![]() ,
,
∴![]() . . .
. . .
(3)情况1:如图,当AD= ![]() 时,取AB的中点M,连结MF和CM,
时,取AB的中点M,连结MF和CM,

∵∠ACB=90°, tan∠BAC=![]() ,且BC= 6,
,且BC= 6,
∴AC=12,AB=![]() .
.
∵M为AB中点,∴CM=![]() ,
,
∵AD= ![]() ,
,
∴AD=![]() .
.
∵M为AB中点,F为BD中点,
∴FM= ![]() = 2.
= 2.
∴当且仅当M、F、C三点共线且M在线段CF上时CF最大,此时CF=CM+FM=![]() .
.
情况2:如图,当AD= ![]() 时,取AB的中点M,连结MF和CM,
时,取AB的中点M,连结MF和CM,

类似于情况1,可知CF的最大值为![]() .
.
. 6分
综合情况1与情况2,可知当点D在靠近点C的
三等分点时,线段CF的长度取得最大值为![]()


科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与直线
与直线![]() 和直线
和直线![]() 分别交于点
分别交于点![]() (
(![]() 在
在![]() 的上方).
的上方).

![]() 直线
直线![]() 和直线
和直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为 ;
的坐标为 ;
![]() 求线段
求线段![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
![]() 点
点![]() 是
是![]() 轴上一动点,且
轴上一动点,且![]() 为等腰直角三角形,求
为等腰直角三角形,求![]() 的值及点
的值及点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
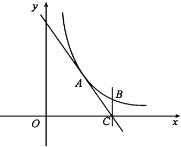
【题目】如图,反比例函数y=![]() (x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线BC交反比例函数图象于点B.
(x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线BC交反比例函数图象于点B.
(1)求k的值与B点的坐标;
(2)在平面内有点D,使得以A,B,C,D四点为顶点的四边形为平行四边形,试写出符合条件的所有D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世纪隆超市举行有奖促销活动:凡一次性购物满300元者即可获得一次摇奖机会。摇奖机是一个圆形转盘,被分成16等分,摇中红、黄、蓝色区域,分获一、二、三获奖,奖金依次为60、50、40元。一次性购物满300元者,如果不摇奖可返还现金15元。

(1)摇奖一次,获一等奖的概率是多少?
(2)摇奖一次,获奖的概率是多少?
(3)老李一次性购物满了300元,他是参与摇奖划算还是领15元现金划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
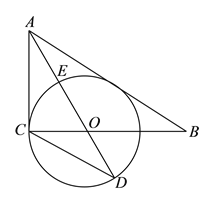
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() 是
是![]() 的角平分线,以
的角平分线,以![]() 为圆心,
为圆心, ![]() 为半径作⊙
为半径作⊙![]() .
.
(![]() )求证:
)求证: ![]() 是⊙
是⊙![]() 的切线.
的切线.
(![]() )已知
)已知![]() 交⊙
交⊙![]() 于点
于点![]() ,延长
,延长![]() 交⊙
交⊙![]() 于点
于点![]() ,
, ![]() ,求
,求![]() 的值.
的值.
(![]() )在(
)在(![]() )的条件下,设⊙
)的条件下,设⊙![]() 的半径为
的半径为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学原计划加工一批校服,现有甲、乙两个工厂加工这批校服,已知甲工厂每天能加工这种校服16件,乙工厂每天加工这种校服24件,且单独加工这批校服甲厂比乙厂要多用20天
(1)求这批校服共有多少件?
(2)为了尽快完成这批校服,若先由甲、乙两工厂按原速度合作一段时间后,甲工厂停工,而乙工厂每天的速度提高25%,乙工厂单独完成剩下的部分,且乙工厂全部工作时间是甲工厂工作时间的2倍还多4天,求乙工厂加工多少天
查看答案和解析>>
科目:初中数学 来源: 题型:
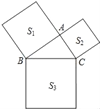
【题目】如图,三角形ABC三边的长分别为AB=m2﹣n2,AC=2mn,BC=m2+n2,其中m、n都是正整数.以AB、AC、BC为边分别向外画正方形,面积分别为S1、S2、S3,那么S1、S2、S3之间的数量关系为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根调查结果绘制成的统计图(部分)如图所示.
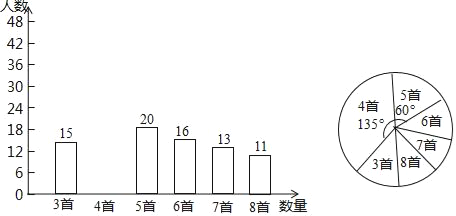
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 10 | 10 | 15 | 40 | 25 | 20 |
请根据调查的信息
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠A=90°.
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明);

(2)在(1)的条件下,若∠B=45°,AB=1,⊙P切BC于点D,求劣弧![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com