
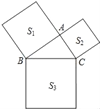
【题目】如图,三角形ABC三边的长分别为AB=m2﹣n2,AC=2mn,BC=m2+n2,其中m、n都是正整数.以AB、AC、BC为边分别向外画正方形,面积分别为S1、S2、S3,那么S1、S2、S3之间的数量关系为_____.
科目:初中数学 来源: 题型:
【题目】由大小相同(棱长为1分米)的小立方块搭成的几何体如下图.


(1)请在右图的方格中画出该几何体的俯视图和左视图;
(2)图中有 块小正方体,它的表面积(含下底面)为 ;
(3)用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何体最少要_______个小立方块,最多要_______个小立方块.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,飞机在一定高度上沿水平直线飞行,先在点![]() 处测得正前方小岛
处测得正前方小岛![]() 的俯角为
的俯角为![]() ,面向小岛方向继续飞行
,面向小岛方向继续飞行![]()
![]() 到达
到达![]() 处,发现小岛在其正后方,此时测得小岛的俯角为
处,发现小岛在其正后方,此时测得小岛的俯角为![]() .如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
.如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,tan∠BAC=![]() . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
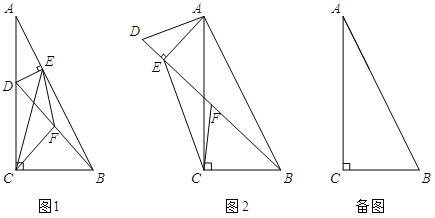
(1)若过点D作DE⊥AB于E,连结CF、EF、CE,如图1.设![]() ,则k= ;
,则k= ;
(2)若将图1中的△ADE绕点A旋转,使得D、E、B三点共线,点F仍为BD中点,如图2所示.求证:BE-DE=2CF;
(3)若BC=6,点D在边AC的三等分点处,将线段AD绕点A旋转,点F始终为BD中点,求线段CF长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】双蓉服装店老板到厂家购A、B两种型号的服装,若购A种型号服装6件,B种型号服装16件,需要1260元;若购进A种型号服装12件,B种型号服装8件,需要1080元。
(1)求A、B两种型号的服装每件分别为多少元?
(2)若销售一件A型服装可获利20元,销售一件B型服装可获利30元,根据市场需要,服装店老板决定:购进A型服装的数量要比购进B型服装的数量的2倍还多4件,且A型服装最多可购进28件,这样服装全部售出后可使总的获利不少于780元,问有几种进货方案?如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,

请回答下列问题:
(1)这次被调查的学生共有多少人?
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,用三种大小不同的5个正方形和一个长方形(阴影部分)拼成长方形ABCD,其中EF=2厘米,最小的正方形的边长为x厘米.
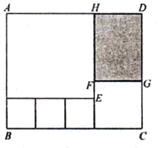
(1)用含x的代数式表示FG=________厘米,DG=________厘米.
(2)若长方形ABCD的周长等于52,求x的值
(3)若FG:DG=2:3,求四边形FGDH(阴影部分)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数 y=kx+b 的图像如图所示,则当kx+b>0 时,x 的取值范围为___________.

【答案】x>1
【解析】分析:题目要求 kx+b>0,即一次函数的图像在x 轴上方时,观察图象即可得x的取值范围.
详解:
∵kx+b>0,
∴一次函数的图像在x 轴上方时,
∴x的取值范围为:x>1.
故答案为:x>1.
点睛:本题考查了一次函数与一元一次不等式的关系,主要考查学生的观察视图能力.
【题型】填空题
【结束】
16
【题目】菱形ABCD中, ![]() ,其周长为32,则菱形面积为____________.
,其周长为32,则菱形面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上有四个点A、B、C、D,请用直尺按下列要求作图:
(1)作直线AB;
(2)作射线BC;
(3)连接AD,并将其反向延长至E,使DE=2AD;
(4)找到一点F,使点F到A、B、C、D四点的距离之和最短.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com