
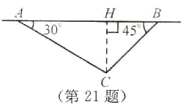
【题目】如图所示,飞机在一定高度上沿水平直线飞行,先在点![]() 处测得正前方小岛
处测得正前方小岛![]() 的俯角为
的俯角为![]() ,面向小岛方向继续飞行
,面向小岛方向继续飞行![]()
![]() 到达
到达![]() 处,发现小岛在其正后方,此时测得小岛的俯角为
处,发现小岛在其正后方,此时测得小岛的俯角为![]() .如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
.如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).

【答案】![]()
【解析】
试题分析:过点C作CH![]() AB,垂足为H,则CH的长度即为飞机飞行的高度.设CH=xkm,在Rt△ACH中,用x表示出AH的长;在Rt△ACH中,∠BHC=90°,可得BH=CH=x,根据为AH+HB=AB=10列出方程,解方程求得x的值,即可得飞机飞行的高度.
AB,垂足为H,则CH的长度即为飞机飞行的高度.设CH=xkm,在Rt△ACH中,用x表示出AH的长;在Rt△ACH中,∠BHC=90°,可得BH=CH=x,根据为AH+HB=AB=10列出方程,解方程求得x的值,即可得飞机飞行的高度.
试题解析:过点C作CH![]() AB,垂足为H,则CH的长度即为飞机飞行的高度.
AB,垂足为H,则CH的长度即为飞机飞行的高度.
设CH=xkm,在Rt△ACH中,∠AHC=90°,∠CAH=30°,
因为tan∠CAH=![]() ,所以AH=
,所以AH=![]() ,
,
又在Rt△ACH中,∠BHC=90°,∠CBH=45°,
所以BH=CH=x
因为AH+HB=AB=10,所以![]() ,
,
解得![]() ,
,
答:飞机飞行的高度为![]()


科目:初中数学 来源: 题型:
【题目】操作:“如图1,P是平面直角坐标系中一点(x轴上的点除外),过点P作PC⊥x轴于点C,点C绕点P逆时针旋转60°得到点Q.”我们将此由点P得到点Q的操作称为点的T变换.
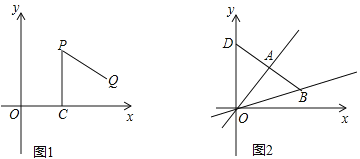
(1)点P(a,b)经过T变换后得到的点Q的坐标为 ;若点M经过T变换后得到点N(6,﹣![]() ),则点M的坐标为 .
),则点M的坐标为 .
(2)A是函数y=![]() x图象上异于原点O的任意一点,经过T变换后得到点B.
x图象上异于原点O的任意一点,经过T变换后得到点B.
①求经过点O,点B的直线的函数表达式;
②如图2,直线AB交y轴于点D,求△OAB的面积与△OAD的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上移动,连接
上移动,连接![]() ,将多边形
,将多边形![]() 沿直线
沿直线![]() 折叠,得到多边形
折叠,得到多边形![]() ,点
,点![]() 、
、![]() 的对应点分别为点
的对应点分别为点![]() 、
、![]() .
.
(1)当![]() 恰好经过点
恰好经过点![]() 时(如图1),求线段
时(如图1),求线段![]() 的长;
的长;
(2)若![]() 分别交边
分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() ,且
,且![]() (如图2),求
(如图2),求![]() 的面积;
的面积;
(3)在点![]() 从点
从点![]() 移动到点
移动到点![]() 的过程中,求点
的过程中,求点![]() 运动的路径长.
运动的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,属于必然事件的是( )
A.明天我市下雨
B.抛一枚硬币,正面朝上
C.走出校门,看到的第一辆汽车的牌照的末位数字是偶数
D.一个口袋中装有2个红球和一个白球,从中摸出2个球,其中有红球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线 ![]() 交x轴、y轴分别于点A、点B,将△AOB绕坐标原点逆时针旋转
交x轴、y轴分别于点A、点B,将△AOB绕坐标原点逆时针旋转 ![]() 得到△COD.直线CD交直线AB于点E,如图1.
得到△COD.直线CD交直线AB于点E,如图1.
图1
(1)求:直线CD的函数关系式.
(2)如图2,连接OE,过点O作 ![]() 交直线CD于点F,如图2.
交直线CD于点F,如图2.
图2
① 求证: ![]() =
= ![]() .
.
② 求:点F的坐标.
(3)若点P是直线DC上一点,点Q是x轴上一点(点Q不与点O重合),当△DPQ和△DOC全等时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽取部分学生做了一次问卷调查,要求学生选出自己喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:
各版面选择人数的扇形统计图 各版面选择人数的条形统计图
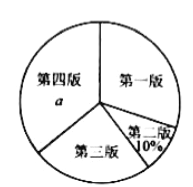

请根据图中信息,解答下列问题:
(1)该调查的样本容量为 ,![]()
![]() ,“第一版”对应扇形的圆心角为
,“第一版”对应扇形的圆心角为 ![]() ;
;
(2)请你补全条形统计图;
(3)若该校有![]() 名学生,请你估计全校学生中最喜欢“第一版”的人数.
名学生,请你估计全校学生中最喜欢“第一版”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方法.如图2,火柴盒的一个侧面ABCD倒下到AEFG的位置,连结CF,AB=a,BC=b,AC=c.
(1)请你结合图1用文字和符号语言分别叙述勾股定理;
(2)请利用直角梯形BCFG的面积证明勾股定理: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
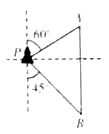
【题目】如图,一艘海轮位于灯塔![]() 的北偏东
的北偏东![]() 方向,距离灯塔
方向,距离灯塔![]() 的
的![]() 处,它沿正南方向航行一段时间后,到达位于灯塔
处,它沿正南方向航行一段时间后,到达位于灯塔![]() 的南偏东
的南偏东![]() 方向上的
方向上的![]() 处.此时,
处.此时,![]() 处与灯塔
处与灯塔![]() 的距离约为
的距离约为 ![]() .(结果取整数,参考数据:
.(结果取整数,参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开展读书月活动,对学生最喜欢的图书种类进行了一次抽样调查,所有图书分成四类:艺术、文学、科普、其他。随机调查了该校![]() 名学生(每名学生必须且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图:
名学生(每名学生必须且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图:
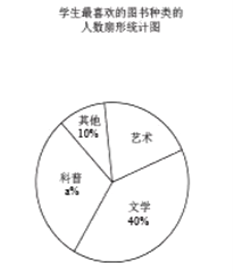
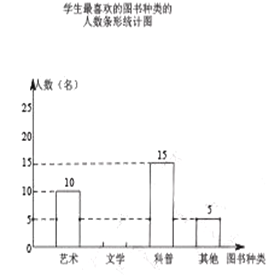
根据统计图提供的信息,解答下列问题:
(1)![]() ,
,![]() ;
;
(2)扇形统计图中,“艺术”所对应的扇形的圆心角度数是 度.
(3)请根据以上信息直接在答题卡中补全条形统计图;
(4)根据抽样调查的结果,请你估计该校600名学生中有多少学生最喜欢科普类图书.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com