
【题目】操作:“如图1,P是平面直角坐标系中一点(x轴上的点除外),过点P作PC⊥x轴于点C,点C绕点P逆时针旋转60°得到点Q.”我们将此由点P得到点Q的操作称为点的T变换.
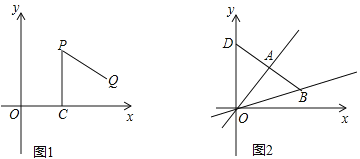
(1)点P(a,b)经过T变换后得到的点Q的坐标为 ;若点M经过T变换后得到点N(6,﹣![]() ),则点M的坐标为 .
),则点M的坐标为 .
(2)A是函数y=![]() x图象上异于原点O的任意一点,经过T变换后得到点B.
x图象上异于原点O的任意一点,经过T变换后得到点B.
①求经过点O,点B的直线的函数表达式;
②如图2,直线AB交y轴于点D,求△OAB的面积与△OAD的面积之比.
【答案】(1)Q(a+![]() b,
b,![]() b);M(9,﹣2
b);M(9,﹣2![]() );(2)①y=
);(2)①y=![]() x;②
x;②![]()
【解析】
试题分析:(1)连接CQ可知△PCQ为等边三角形,过Q作QD⊥PC,利用等边三角形的性质可求得CD和QD的长,则可求得Q点坐标;设出M点的坐标,利用P、Q坐标之间的关系可得到点M的方程,可求得M点的坐标;
(2)①可取A(2,![]() ),利用T变换可求得B点坐标,利用待定系数示可求得直线OB的函数表达式;②由待定系数示可求得直线AB的解析式,可求得D点坐标,则可求得AB、AD的长,可求得△OAB的面积与△OAD的面积之比.
),利用T变换可求得B点坐标,利用待定系数示可求得直线OB的函数表达式;②由待定系数示可求得直线AB的解析式,可求得D点坐标,则可求得AB、AD的长,可求得△OAB的面积与△OAD的面积之比.
试题解析:(1)如图1,连接CQ,过Q作QD⊥PC于点D,
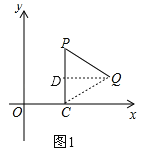
由旋转的性质可得PC=PQ,且∠CPQ=60°,
∴△PCQ为等边三角形,
∵P(a,b),
∴OC=a,PC=b,
∴CD=![]() PC=
PC=![]() b,DQ=
b,DQ=![]() PQ=
PQ=![]() b,
b,
∴Q(a+![]() b,
b,![]() b);
b);
设M(x,y),则N点坐标为(x+![]() y,
y,![]() y),
y),
∵N(6,﹣![]() ),
),
∴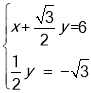 ,解得
,解得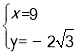 ,
,
∴M(9,﹣2![]() );
);
(2)①∵A是函数y=![]() x图象上异于原点O的任意一点,
x图象上异于原点O的任意一点,
∴可取A(2,![]() ),
),
∴2+![]() ×
×![]() =
=![]() ,
,![]() ×
×![]() =
=![]() ,
,
∴B(![]() ,
,![]() ),
),
设直线OB的函数表达式为y=kx,则![]() k=
k=![]() ,解得k=
,解得k=![]() ,
,
∴直线OB的函数表达式为y=![]() x;
x;
②设直线AB解析式为y=k′x+b,
把A、B坐标代入可得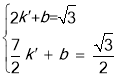 ,解得
,解得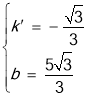 ,
,
∴直线AB解析式为y=﹣![]() x+
x+![]() ,
,
∴D(0,![]() ),且A(2,
),且A(2,![]() ),B(
),B(![]() ,
,![]() ),
),
∴AB=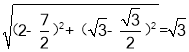 ,AD=
,AD=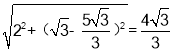 ,
,
∴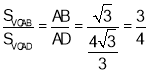 .
.


科目:初中数学 来源: 题型:
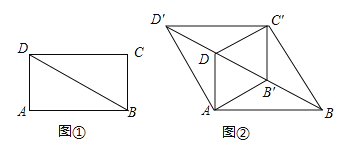
【题目】如图①,BD是矩形ABCD的对角线,∠ABD=30°,AD=1.将△BCD沿射线BD方向平移到△B'C'D'的位置,使B'为BD中点,连接AB',C'D,AD',BC',如图②.
(1)求证:四边形AB'C'D是菱形;
(2)四边形ABC'D′的周长为 ;
(3)将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,将△ADC绕点A顺时针旋转,使AC与AB重合,点D落在点E处,AE的延长线交CB的延长线于点M,EB的延长线交AD的延长线于点N.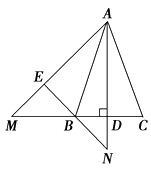
求证:AM=AN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,飞机在一定高度上沿水平直线飞行,先在点![]() 处测得正前方小岛
处测得正前方小岛![]() 的俯角为
的俯角为![]() ,面向小岛方向继续飞行
,面向小岛方向继续飞行![]()
![]() 到达
到达![]() 处,发现小岛在其正后方,此时测得小岛的俯角为
处,发现小岛在其正后方,此时测得小岛的俯角为![]() .如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
.如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com