
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,将△ADC绕点A顺时针旋转,使AC与AB重合,点D落在点E处,AE的延长线交CB的延长线于点M,EB的延长线交AD的延长线于点N.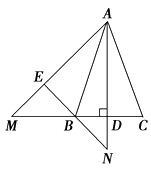
求证:AM=AN.
科目:初中数学 来源: 题型:
【题目】综合题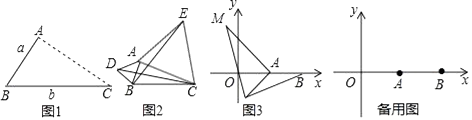
(1)问题
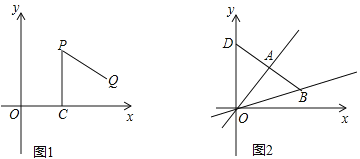
如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于时,线段AC的长取得最大值,且最大值为(用含a,b的式子表示)
(2)应用
点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90,请直接写出线段AM长的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠ABC=60°,AB=8cm,D是AB的中点.现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M点.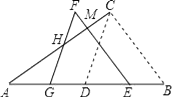
(1)求证:AG=GH;
(2)求四边形GHME的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
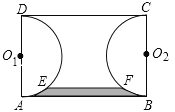
【题目】如图,已知矩形ABCD中,AB=3,AD=2,分别以边AD,BC为直径在矩形ABCD的内部作半圆O1和半圆O2,一平行于AB的直线EF与这两个半圆分别交于点E、点F,且EF=2(EF与AB在圆心O1和O2的同侧),则由![]() ,EF,
,EF,![]() ,AB所围成图形(图中阴影部分)的面积等于 .
,AB所围成图形(图中阴影部分)的面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作:“如图1,P是平面直角坐标系中一点(x轴上的点除外),过点P作PC⊥x轴于点C,点C绕点P逆时针旋转60°得到点Q.”我们将此由点P得到点Q的操作称为点的T变换.
(1)点P(a,b)经过T变换后得到的点Q的坐标为 ;若点M经过T变换后得到点N(6,﹣![]() ),则点M的坐标为 .
),则点M的坐标为 .
(2)A是函数y=![]() x图象上异于原点O的任意一点,经过T变换后得到点B.
x图象上异于原点O的任意一点,经过T变换后得到点B.
①求经过点O,点B的直线的函数表达式;
②如图2,直线AB交y轴于点D,求△OAB的面积与△OAD的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地新建的一个企业,每月将生产1960吨污水,为保护环境,该企业计划购置污水处理器,并在如下两个型号种选择:
污水处理器型号 | A型 | B型 |
处理污水能力(吨/月) | 240 | 180 |
已知商家售出的2台A型、3台B型污水处理器的总价为44万元,售出的1台A型、4台B型污水处理器的总价为42万元.
(1)求每台A型、B型污水处理器的价格;
(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么他们至少要支付多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽取部分学生做了一次问卷调查,要求学生选出自己喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:
各版面选择人数的扇形统计图 各版面选择人数的条形统计图
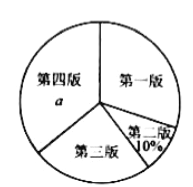

请根据图中信息,解答下列问题:
(1)该调查的样本容量为 ,![]()
![]() ,“第一版”对应扇形的圆心角为
,“第一版”对应扇形的圆心角为 ![]() ;
;
(2)请你补全条形统计图;
(3)若该校有![]() 名学生,请你估计全校学生中最喜欢“第一版”的人数.
名学生,请你估计全校学生中最喜欢“第一版”的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com