
【题目】如图,△ABC中,∠ACB=90°,∠ABC=60°,AB=8cm,D是AB的中点.现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M点.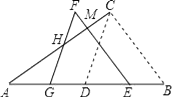
(1)求证:AG=GH;
(2)求四边形GHME的面积.
【答案】
(1)证明:将△BCD沿BA方向平移得到△EFG,
∴△BCD≌△EFG,FG∥CD,EF∥CB,DG=EB=1,
∵∠ACB=90°,D是AB的中点,
∴AD=CD=BD= ![]() AB=
AB= ![]() ×8=4,
×8=4,
∴∠DAC=∠ACD,
∵FG∥CD,
∴∠AFG=∠ACD,
∴∠AHG=∠DAC,
∴AG=GH
(2)解:如图:过C作CN⊥AB于N,

∵∠ABC=60°,∠ACB=90°,
∵BC= ![]() AB=
AB= ![]() ×8=4,
×8=4,
∵∠ABC=60°,CD=BD,
∴△BCD为等边三角形,
∴NB= ![]() BD=2,
BD=2,
∴CN= ![]() ,
,
∵DG=1,AD=4,
∴GH=AG=3,
∴FH=1,you
∵∠A=30°,
∴∠A=30°=∠AHG=∠FHM=30°,
∵FE∥CB,∠ACB=90°,
∴MF= ![]() ,
,
∴HM= ![]() .
.
∴S△EFG=S△BCD= ![]() ×4×2
×4×2 ![]() =4
=4 ![]() ,
,
S△MFH= ![]() ×
× ![]() ×
× ![]() =
= ![]() ,
,
【解析】(1)由点D是直角三角形的斜边AB的中点,得到CD=AD=DB,根据等边对等角,得出∠A=∠ACD,由平移得到FG∥CD,则可得∠AHG=∠ACD,即可得∠AHG=∠A,等角对等边得到AG=GH;(2)四边形GHME是由直角三角形AME减去等腰三角形AGH得到的。


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点C为直线y=x上在第一象限内一点,直线y=2x+1交y轴于点A,交x轴于B,将直线AB沿射线OC方向平移 ![]() 个单位,则平移后直线的解析式为。
个单位,则平移后直线的解析式为。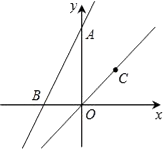
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形玻璃杯,高为11cm,底面周长为16cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 . (结果保留根号)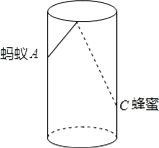
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,BD是矩形ABCD的对角线,∠ABD=30°,AD=1.将△BCD沿射线BD方向平移到△B'C'D'的位置,使B'为BD中点,连接AB',C'D,AD',BC',如图②.
(1)求证:四边形AB'C'D是菱形;
(2)四边形ABC'D′的周长为 ;
(3)将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
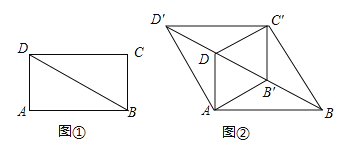
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A.2a3÷a2=a
B.a2+a2=a4
C.(2a+b)2=4a2+b2+4ab
D.(2a+1)(2a﹣1)=2a2﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,将△ADC绕点A顺时针旋转,使AC与AB重合,点D落在点E处,AE的延长线交CB的延长线于点M,EB的延长线交AD的延长线于点N.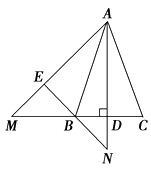
求证:AM=AN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强与小刚都住在安康小区,在同一所学校读书.某天早上,小强![]() 从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留
从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留![]() 分钟,校车行驶途中始终保持匀速.当天早上,小刚
分钟,校车行驶途中始终保持匀速.当天早上,小刚![]() 从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早
从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早![]() 分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程
分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程![]() (千米)与行驶时间
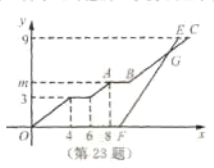
(千米)与行驶时间![]() (分钟)之间的函数图象如图所示.
(分钟)之间的函数图象如图所示.
(1)求点![]() 的纵坐标
的纵坐标![]() 的值;
的值;
(2)小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车?并求此时他们距学校站点的路程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com