
【题目】如图,已知点C为直线y=x上在第一象限内一点,直线y=2x+1交y轴于点A,交x轴于B,将直线AB沿射线OC方向平移 ![]() 个单位,则平移后直线的解析式为。
个单位,则平移后直线的解析式为。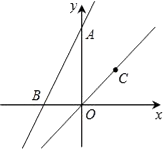
【答案】y=2x
【解析】设点A沿射线OC方向平移 ![]() 个单位后到达点M,点B沿射线OC方向平移
个单位后到达点M,点B沿射线OC方向平移 ![]() 个单位后到达点N,过点M作ME⊥y轴于点M,过点N作NF⊥x轴于点F,如图所示.
个单位后到达点N,过点M作ME⊥y轴于点M,过点N作NF⊥x轴于点F,如图所示.

∵直线OC的解析式为y=x,
∴∠COF=∠COA=45°.
∵AM∥OC、BN∥OC,
∴∠NBF=∠COF=45°,∠MAE=∠COA=45°,
∴△AEM和△BFN为等腰直角三角形,且AM=BN= ![]() ,
,
∴BF=NF=AE=EM=1.
当x=0时,y=2x+1=1,
∴点A的坐标为(0,1);
当y=2x+1=0时,x=﹣ ![]() ,
,
∴点B的坐标为(﹣ ![]() ,0).
,0).
∴点M的坐标为(1,2),点N的坐标为( ![]() ,1).
,1).
设直线MN的解析式为y=kx+b,
将M(1,2)、N( ![]() ,1)代入y=kx+b,
,1)代入y=kx+b,
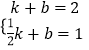 ,解得:
,解得: ![]() ,
,
∴直线MN的解析式为y=2x.
故答案为:y=2x.
先画出平移后的图像,设设点A沿射线OC方向平移 ![]() 个单位后到达点M,点B沿射线OC方向平移
个单位后到达点M,点B沿射线OC方向平移![]() 个单位后到达点N,过点M作ME⊥y轴于点M,过点N作NF⊥x轴于点F,根据直线OC的解析式为直线y=x及AM∥OC、BN∥OC,可证出∠NBF=∠COF=∠MAE=∠COA=45°,平移的距离为AM=BN=
个单位后到达点N,过点M作ME⊥y轴于点M,过点N作NF⊥x轴于点F,根据直线OC的解析式为直线y=x及AM∥OC、BN∥OC,可证出∠NBF=∠COF=∠MAE=∠COA=45°,平移的距离为AM=BN= ![]() ,利用勾股定理求出BF=NF=AE=EM=1,再求出直线y=2x+1与x轴和y轴的交点坐标,从而得出点M、N的坐标,然后利用待定系数法求出直线MN的函数解析式。
,利用勾股定理求出BF=NF=AE=EM=1,再求出直线y=2x+1与x轴和y轴的交点坐标,从而得出点M、N的坐标,然后利用待定系数法求出直线MN的函数解析式。


科目:初中数学 来源: 题型:
【题目】在△ABC内一点P满足PA=PB=PC,则点P一定是△ABC的( )
A. 三边垂直平分线的交点 B. 三条内角平分线的交点
C. 三条高的交点 D. 三条中线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )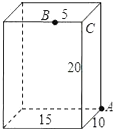
A.5 ![]()
B.25
C.10 ![]() +5
+5
D.35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)
问题背景:已知![]() 的顶点
的顶点![]() 在
在![]() 的边
的边![]() 所在直线上(不与
所在直线上(不与![]() ,
,![]() 重合).
重合).![]() 交
交![]() 所在直线于点
所在直线于点![]() ,
,![]() 交
交![]() 所在直线于点
所在直线于点![]() .记
.记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() .
.
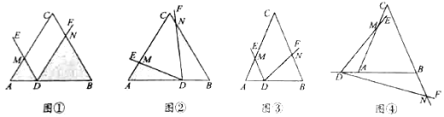
(1)初步尝试:如图①,当![]() 是等边三角形,
是等边三角形,![]() ,
,![]() ,且
,且![]() ,
,![]() 时,则
时,则![]() ;
;
(2)类比探究:在(1)的条件下,先将点![]() 沿
沿![]() 平移,使
平移,使![]() ,再将
,再将![]() 绕点
绕点![]() 旋转至如图②所示位置,求
旋转至如图②所示位置,求![]() 的值;
的值;
(3)延伸拓展:当![]() 是等腰三角形时,设
是等腰三角形时,设![]() .
.
(I)如图③,当点![]() 在线段
在线段![]() 上运动时,设
上运动时,设![]() ,
,![]() ,求
,求![]() 的表达式(结果用
的表达式(结果用![]() ,
,![]() 和
和![]() 的三角函数表示).
的三角函数表示).
(II)如图④,当点![]() 在
在![]() 的延长线上运动时,设
的延长线上运动时,设![]() ,
,![]() ,直接写出
,直接写出![]() 的表达式,不必写出解答过程.
的表达式,不必写出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题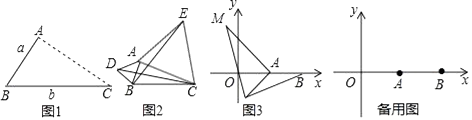
(1)问题
如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于时,线段AC的长取得最大值,且最大值为(用含a,b的式子表示)
(2)应用
点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90,请直接写出线段AM长的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠ABC=60°,AB=8cm,D是AB的中点.现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M点.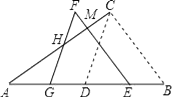
(1)求证:AG=GH;
(2)求四边形GHME的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com