练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，圆柱形玻璃杯，高为11cm，底面周长为16cm，在杯内离杯底3cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为 ． （结果保留根号）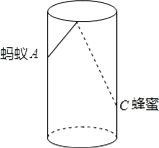

    【答案】15cm
    【解析】如图，

    将杯子侧面展开，作A关于EF的对称点A′，

    连接A′C，则A′C即为最短距离，

    A′C2=A′D2+CD2

    =92+122

    =225，

    ∴CA′=15cm

    答：蚂蚁到达蜂蜜的最短距离的是15cm．

    所以答案是15cm．

    【考点精析】本题主要考查了线段的基本性质和圆柱的相关计算的相关知识点，需要掌握线段公理：所有连接两点的线中，线段最短．也可简单说成：两点之间线段最短；连接两点的线段的长度，叫做这两点的距离；线段的大小关系和它们的长度的大小关系是一致的；圆柱的体积： V圆柱=πR2h才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】要判断一个学生的数学考试成绩是否稳定，那么需要知道他最近连续几次数学考试成绩的（ ）
    A.方差
    B.平均数
    C.中位数
    D.众数

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列运算中，正确的是（　　）

    A.5a+3b＝8abB.4a3+2a2＝6a5

    C.8b2﹣7b2＝1D.6ab2﹣6b2a＝0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合题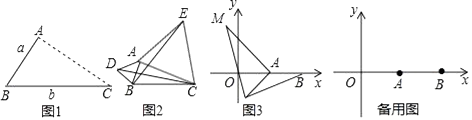

    （1）问题
    如图1，点A为线段BC外一动点，且BC=a，AB=b．
    填空：当点A位于时，线段AC的长取得最大值，且最大值为（用含a，b的式子表示）
    （2）应用
    点A为线段BC外一动点，且BC=3，AB=1，如图2所示，分别以AB，AC为边，作等边三角形ABD和等边三角形ACE，连接CD，BE．
    ①请找出图中与BE相等的线段，并说明理由；
    ②直接写出线段BE长的最大值．
    （3）拓展：如图3，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（5，0），点P为线段AB外一动点，且PA=2，PM=PB，∠BPM=90，请直接写出线段AM长的最大值及此时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列各数中，不是无理数的是（ ）
    A.
    B.0.5
    C.2π
    D.0.151151115…（两个5之间依次多1个1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知在平面直角坐标系中有三点A（﹣2，1）、B（3，1）、C（2，3）．请回答如下问题：

    （1）①在坐标系内描出点A、B、C的位置，并求△ABC的面积；②在平面直角坐标系中画出△A′B′C′，使它与△ABC关于x轴对称，并写出△A′B′C′三顶点的坐标；
    （2）若M（x，y）是△ABC内部任意一点，请直接写出这点在△A′B′C′内部的对应点M′的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题是假命题的是 （ ）

    A. 四个角相等的四边形是矩形 B. 对角线互相平分的四边形是平行四边形

    C. 对角线垂直的四边形是菱形 D. 对角线垂直且相等的平行四边形是正方形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠ACB=90°，∠ABC=60°，AB=8cm，D是AB的中点．现将△BCD沿BA方向平移1cm，得到△EFG，FG交AC于H，FE交AC于M点．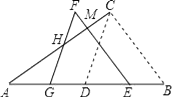

    （1）求证：AG=GH；
    （2）求四边形GHME的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：（x2+px+2）（x﹣1）的结果中不含x的二次项，求p2017的值．

    查看答案和解析>>

    同步练习册答案