
【题目】一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方法.如图2,火柴盒的一个侧面ABCD倒下到AEFG的位置,连结CF,AB=a,BC=b,AC=c.
(1)请你结合图1用文字和符号语言分别叙述勾股定理;
(2)请利用直角梯形BCFG的面积证明勾股定理: ![]() .
.
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图所示,飞机在一定高度上沿水平直线飞行,先在点![]() 处测得正前方小岛
处测得正前方小岛![]() 的俯角为
的俯角为![]() ,面向小岛方向继续飞行
,面向小岛方向继续飞行![]()
![]() 到达
到达![]() 处,发现小岛在其正后方,此时测得小岛的俯角为
处,发现小岛在其正后方,此时测得小岛的俯角为![]() .如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
.如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.(友情提醒:正方形的四条边都相等,即AB=BC=CD=DA;四个内角都是90°,即∠A=∠B=∠C=∠D=90°)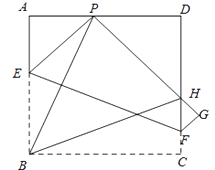
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;
(3)设AP为x,求出BE的长.(用含x的代数式表式)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.
(1)求证:BC是⊙F的切线;
(2)若点A、D的坐标分别为A(0,﹣1),D(2,0),求⊙F的半径;
(3)试探究线段AG、AD、CD三者之间满足的等量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夏季空调销售供不应求,某空调厂接到一份紧急订单,要求在10天内(含10天)完成任务,为提高生产效率,工厂加班加点,接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,由于机器损耗等原因,当日生产的空调数量达到50台后,每多生产一台,当天生产的所有空调,平均每台成本就增加20元.
(1)设第![]() 天生产空调
天生产空调![]() 台,直接写出
台,直接写出![]() 与
与![]() 之间的函数解析式,并写出自变量
之间的函数解析式,并写出自变量![]() 的取值范围.
的取值范围.
(2)若每台空调的成本价(日生产量不超过50台时)为2000元,订购价格为每台2920元,设第![]() 天的利润为
天的利润为![]() 元,试求
元,试求![]() 与
与![]() 之间的函数解析式,并求工厂哪一天获得的利润最大,最大利润是多少.
之间的函数解析式,并求工厂哪一天获得的利润最大,最大利润是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com