
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§“―÷Σ≈ΉΈοœΏ![]() ΒΡΆΦœσΨ≠ΙΐΒψ
ΒΡΆΦœσΨ≠ΙΐΒψ![]() Θ§
Θ§![]() Θ§ΤδΕ‘≥Τ÷αΈΣ÷±œΏ
Θ§ΤδΕ‘≥Τ÷αΈΣ÷±œΏ![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής
Ής![]() ÷αΫΜ≈ΉΈοœΏ”ΎΒψ
÷αΫΜ≈ΉΈοœΏ”ΎΒψ![]() Θ§
Θ§![]() ΒΡΤΫΖ÷œΏΫΜœΏΕΈ
ΒΡΤΫΖ÷œΏΫΜœΏΕΈ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Βψ
Θ§Βψ![]() «≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘ§…ηΤδΚαΉχ±ξΈΣ
«≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘ§…ηΤδΚαΉχ±ξΈΣ![]() Θ°
Θ°
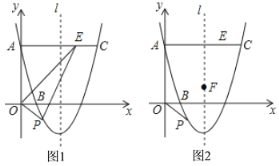
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©»τΕ·Βψ![]() ‘Ύ
‘Ύ![]() ΓΔ
ΓΔ![]() ΦδΒΡ≈ΉΈοœΏ…œΘ§Ν§Ϋα
ΦδΒΡ≈ΉΈοœΏ…œΘ§Ν§Ϋα![]() Θ§
Θ§![]() Θ§«σΥΡ±Ώ–Έ
Θ§«σΥΡ±Ώ–Έ![]() ΟφΜΐ
ΟφΜΐ![]() ”κ
”κ![]() ÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®3Θ©»γΆΦ2Θ§![]() «≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œΒΡ“ΜΒψΘ§‘ΎΕ‘≥Τ÷αΉσ≤ύΒΡ≈ΉΈοœΏ…œ «Ζώ¥φ‘ΎΒψ
«≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œΒΡ“ΜΒψΘ§‘ΎΕ‘≥Τ÷αΉσ≤ύΒΡ≈ΉΈοœΏ…œ «Ζώ¥φ‘ΎΒψ![]() Ι
Ι![]() ≥…ΈΣ“‘Βψ
≥…ΈΣ“‘Βψ![]() ΈΣ÷±Ϋ«ΕΞΒψΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§÷±Ϋ”–¥≥ωΥυ”–ΖϊΚœΧθΦΰΒΡΒψ
ΈΣ÷±Ϋ«ΕΞΒψΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§÷±Ϋ”–¥≥ωΥυ”–ΖϊΚœΧθΦΰΒΡΒψ![]() ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©Βψ
ΘΜΘ®3Θ©Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ Μρ
Μρ Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ© Ήœ»ΗυΨίΕ‘≥Τ–‘ΒΟ≥ω≈ΉΈοœΏ”κ![]() ÷αΒΡΝμ“ΜΗωΫΜΒψΉχ±ξΘ§»ΜΚσΗυΨίΝΫΉχ±ξ…η≈ΉΈοœΏΫβΈω ΫΘ§¥ζ»κΒψAΒΡΉχ±ξΘ§Φ¥Ω…ΒΟΫβΘΜ
÷αΒΡΝμ“ΜΗωΫΜΒψΉχ±ξΘ§»ΜΚσΗυΨίΝΫΉχ±ξ…η≈ΉΈοœΏΫβΈω ΫΘ§¥ζ»κΒψAΒΡΉχ±ξΘ§Φ¥Ω…ΒΟΫβΘΜ
Θ®2Θ© Ήœ»…η![]() Θ§ΗυΨίΫ«ΤΫΖ÷œΏΒΡ–‘÷ ΒΟ≥ωΓςAOE «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§»ΜΚσΫΪΥΡ±Ώ–ΈΖ÷≥…ΝΫΗω»ΐΫ«–Έ«σΫβΦ¥Ω…ΒΟ≥ωΚ· ΐΙΊœΒ ΫΘΜ
Θ§ΗυΨίΫ«ΤΫΖ÷œΏΒΡ–‘÷ ΒΟ≥ωΓςAOE «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§»ΜΚσΫΪΥΡ±Ώ–ΈΖ÷≥…ΝΫΗω»ΐΫ«–Έ«σΫβΦ¥Ω…ΒΟ≥ωΚ· ΐΙΊœΒ ΫΘΜ
Θ®3Θ©¥φ‘ΎΝΫ÷÷«ιΩωΘΚ»γΆΦΥυ ΨΘ§ΉςΗ®÷ζœΏΙΙΫ®»ΪΒ»»ΐΫ«–ΈΘ§ΗυΨί![]() Θ§Ν–ΖΫ≥ΧΦ¥Ω…ΒΟ≥ωΒψPΒΡΉχ±ξ.
Θ§Ν–ΖΫ≥ΧΦ¥Ω…ΒΟ≥ωΒψPΒΡΉχ±ξ.
Θ®1Θ©»γΆΦΘ§…η≈ΉΈοœΏ”κ![]() ÷αΒΡΝμ“ΜΗωΫΜΒψΈΣ
÷αΒΡΝμ“ΜΗωΫΜΒψΈΣ![]()
”…Ε‘≥Τ–‘ΒΟΘΚ![]()
…η≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚ![]()
Α―![]() ¥ζ»κΒΟΘΚ
¥ζ»κΒΟΘΚ![]()
![]()
![]() ≈ΉΈοœΏΒΡΫβΈω ΫΘΚ
≈ΉΈοœΏΒΡΫβΈω ΫΘΚ![]()
Θ®2Θ©»γΆΦΘ§…η![]()
![]() ΤΫΖ÷
ΤΫΖ÷![]() Θ§
Θ§![]()
![]()
![]() «Β»―ϋ÷±Ϋ«»ΐΫ«–Έ
«Β»―ϋ÷±Ϋ«»ΐΫ«–Έ
![]()
![]()
![]() Θ§
Θ§
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]() Θ°
Θ°
Θ®3Θ©Ζ÷ΝΫ÷÷«ιΩωΘΚ
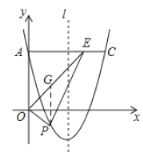
ΔΌΒ±P‘Ύ![]() ÷αœ¬ΖΫ ±Θ§ΙΐΒψPΉςMNΓΆ
÷αœ¬ΖΫ ±Θ§ΙΐΒψPΉςMNΓΆ![]() ÷αΘ§ΫΜ
÷αΘ§ΫΜ![]() ÷α”ΎMΘ§ΫΜΕ‘≥Τ÷α”ΎNΘ§»γΆΦΥυ ΨΘΚ
÷α”ΎMΘ§ΫΜΕ‘≥Τ÷α”ΎNΘ§»γΆΦΥυ ΨΘΚ
ΓΏΓςPOF «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§«“OP=PF
“ΉΒΟΓςOMPΓ’ΓςPNFΘ§
ΓύOM=PN
ΓΏ![]()
‘ρ![]()
ΫβΒΟ![]() Θ®…α»ΞΘ©Μρ
Θ®…α»ΞΘ©Μρ![]()
ΓύΒψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ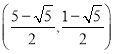
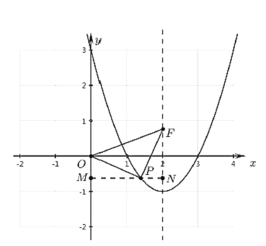
ΔΎΒ±P‘Ύ![]() ÷α…œΖΫ ±Θ§»γΆΦΥυ ΨΘΚ
÷α…œΖΫ ±Θ§»γΆΦΥυ ΨΘΚ
Ά§άμΘ§ΒΟ![]()
ΫβΒΟ![]() Μρ
Μρ![]() Θ®…α»ΞΘ©
Θ®…α»ΞΘ©
ΓύΒψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ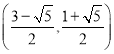
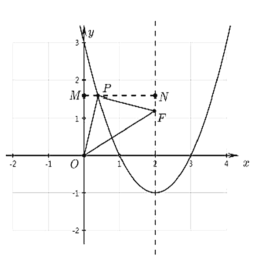
Ήέ…œΘ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ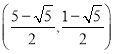 Μρ
Μρ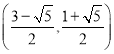 .
.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΕΰ¥ΈΚ· ΐ![]() Θ®kΘΨ0Θ©Θ°
Θ®kΘΨ0Θ©Θ°
Θ®1Θ©Β±k=![]() ±Θ§«σ’βΗωΕΰ¥ΈΚ· ΐΒΡΕΞΒψΉχ±ξΘΜ
±Θ§«σ’βΗωΕΰ¥ΈΚ· ΐΒΡΕΞΒψΉχ±ξΘΜ
Θ®2Θ©«σ÷ΛΘΚΙΊ”ΎxΒΡ“Μ‘Σ¥ΈΖΫ≥Χ![]() ”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυΘΜ
”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυΘΜ
Θ®3Θ©»γΆΦΘ§ΗΟΕΰ¥ΈΚ· ΐ”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ®AΒψ‘ΎBΒψΒΡΉσ≤ύΘ©Θ§”κy÷αΫΜ”ΎCΒψΘ§P «y÷αΗΚΑκ÷α…œ“ΜΒψΘ§«“OP=1Θ§÷±œΏAPΫΜBC”ΎΒψQΘ§«σ÷ΛΘΚ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ≈ΉΈοœΏ![]() Ψ≠ΙΐΒψ
Ψ≠ΙΐΒψ![]() ΚΆΒψ
ΚΆΒψ![]() Θ§”κ
Θ§”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() .
.
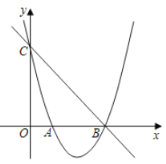
Θ®1Θ©«σ¥Υ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©»τΒψ![]() «÷±œΏ
«÷±œΏ![]() œ¬ΖΫΒΡ≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ®≤ΜΒψ
œ¬ΖΫΒΡ≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ®≤ΜΒψ![]() Θ§
Θ§![]() ÷ΊΚœΘ©Θ§ΙΐΒψ
÷ΊΚœΘ©Θ§ΙΐΒψ![]() Ής
Ής![]() ÷αΒΡΤΫ––œΏΫΜ÷±œΏ
÷αΒΡΤΫ––œΏΫΜ÷±œΏ![]() ”ΎΒψ
”ΎΒψ![]() Θ§…ηΒψ
Θ§…ηΒψ![]() ΒΡΚαΉχ±ξΈΣ
ΒΡΚαΉχ±ξΈΣ![]() .
.
ΔΌ”ΟΚ§![]() ΒΡ¥ζ ΐ Ϋ±μ ΨœΏΕΈ
ΒΡ¥ζ ΐ Ϋ±μ ΨœΏΕΈ![]() ΒΡ≥ΛΘΜ
ΒΡ≥ΛΘΜ
ΔΎΝ§Ϋ”![]() Θ§
Θ§![]() Θ§«σ
Θ§«σ![]() ΒΡΟφΜΐΉν¥σ ±Βψ
ΒΡΟφΜΐΉν¥σ ±Βψ![]() ΒΡΉχ±ξΘΜ
ΒΡΉχ±ξΘΜ
Θ®3Θ©…η≈ΉΈοœΏΒΡΕ‘≥Τ÷α”κ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§Βψ
Θ§Βψ![]() «≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œ“ΜΒψΘ§
«≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œ“ΜΒψΘ§![]() ΈΣ
ΈΣ![]() ÷α…œ“ΜΒψΘ§ «Ζώ¥φ‘Ύ’β―υΒΡΒψ
÷α…œ“ΜΒψΘ§ «Ζώ¥φ‘Ύ’β―υΒΡΒψ![]() ΚΆΒψ
ΚΆΒψ![]() Θ§ ΙΒΟ“‘Βψ
Θ§ ΙΒΟ“‘Βψ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «Νβ–ΈΘΩ»γΙϊ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΒψ
ΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «Νβ–ΈΘΩ»γΙϊ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΒψ![]() ΒΡΉχ±ξΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΒΡΉχ±ξΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΙΪΥΨΡβ”Ο‘Υ”Σ÷Η ΐyά¥ΝΩΜ·ΩΦΚΥΥΨΜζΒΡΙΛΉς“ΒΦ®Θ§‘Υ”Σ÷Η ΐΘ®yΘ©”κ‘Υ δ¥Έ ΐΘ®nΘ©ΚΆΤΫΨυΥΌΕ»Θ®xΘ©÷°Φδ¬ζΉψΙΊœΒ ΫΈΣy=ax2ΘΪbnxΘΪ100Θ§Β±n=1,x=30 ±Θ§y=190ΘΜΒ±n=2Θ§x=40 ±Θ§y=420
”ΟΚ§xΚΆnΒΡ ΫΉ”±μ ΨyΘΜ
Β±‘Υ δ¥Έ ΐΕ®ΈΣ3¥ΈΘ§«σΜώΒΟΉν¥σ‘Υ”Σ÷Η ΐ ±ΒΡΤΫΨυΥΌΕ»ΘΜ
»τn=2,x=40,ΡήΖώ‘Ύn‘ωΦ”m%Θ®mΘΨ0Θ©,Ά§ ±xΦθ…Όm%ΒΡ«ιΩωœ¬Θ§ΕχyΒΡ÷Β±Θ≥÷≤Μ±δΘ§»τΡήΘ§«σ≥ωmΒΡ÷ΒΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”…Θ°
≤ΈΩΦΙΪ ΫΘΚ≈ΉΈοœΏy=ax2ΘΪbxΘΪcΘ®aΓΌ0Θ©ΒΡΕΞΒψΉχ±ξ «Θ®Θ≠![]() Θ§
Θ§![]() Θ©
Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
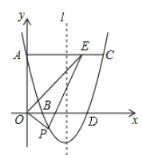
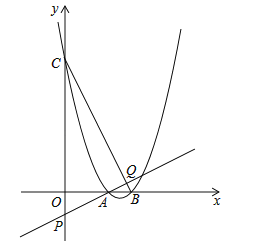
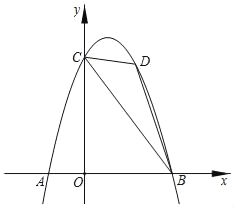
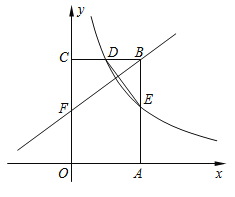
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏy=ax2+bx+6Ψ≠ΙΐΒψAΘ®©¹2Θ§0Θ©Θ§BΘ®4Θ§0Θ©ΝΫΒψΘ§”κy÷αΫΜ”ΎΒψCΘ§ΒψD «≈ΉΈοœΏ…œ“ΜΗωΕ·ΒψΘ§…ηΒψDΒΡΚαΉχ±ξΈΣmΘ®1ΘΦmΘΦ4Θ©Ν§Ϋ”BCΘ§DBΘ§DCΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΚ· ΐΫβΈω ΫΘΜ
Θ®2Θ©ΓςBCDΒΡΟφΜΐ «Ζώ¥φ‘ΎΉν¥σ÷ΒΘ§»τ¥φ‘ΎΘ§«σ¥Υ ±ΒψDΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…ΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§»τΒψM «x÷α…œ“ΜΕ·ΒψΘ§ΒψN «≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ§ ‘≈–Εœ «Ζώ¥φ‘Ύ’β―υΒΡΒψMΘ§ ΙΒΟ“‘ΒψBΘ§DΘ§MΘ§NΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–ΈΘ°»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΒψMΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
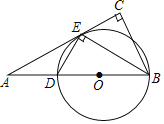
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœC=90ΓψΘ§BEΤΫΖ÷ΓœABCΫΜAC”ΎΒψEΘ§ΉςEDΓΆEBΫΜAB”ΎΒψDΘ§Γ―O «ΓςBEDΒΡΆβΫ”‘≤Θ°
Θ®1Θ©«σ÷ΛΘΚAC «Γ―OΒΡ«–œΏΘΜ
Θ®2Θ©“―÷ΣΓ―OΒΡΑκΨΕΈΣ2.5Θ§BE=4Θ§«σBCΘ§ADΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ’ΐΖΫ–ΈABCD÷–Θ§ΒψP «CD…œ“ΜΕ·ΒψΘ§Ν§ΫαPAΘ§Ζ÷±πΙΐΒψBΓΔDΉςBEΓΆPAΓΔDFΓΆPAΘ§¥ΙΉψΈΣEΓΔFΘ§»γΆΦΔΌΘ°
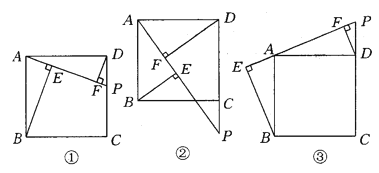
Θ®1Θ©«κΧΫΥςBEΓΔDFΓΔEF’β»ΐΧθœΏΕΈ≥ΛΕ»ΨΏ”–‘θ―υΒΡ ΐΝΩΙΊœΒΘ§»τΒψP‘ΎDCΒΡ―”≥ΛœΏ…œΘ®»γΆΦΔΎΘ©Θ§Ρ«Ο¥’β»ΐΧθœΏΕΈΒΡ≥ΛΕ»÷°Φδ”÷”–‘θ―υΒΡ ΐΝΩΙΊœΒΘΩ»τΒψP‘ΎCDΒΡ―”≥ΛœΏ…œΡΊΘ®»γΆΦΔέΘ©ΘΩ«κΖ÷±π÷±Ϋ”–¥≥ωΫα¬έΘ°
Θ®2Θ©«κ‘ΎΘ®1Θ©÷–ΒΡ»ΐΗωΫα¬έ÷–―Γ‘ώ“ΜΗωΦ”“‘÷ΛΟςΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥≥§ –“‘20‘Σ/«ßΩΥΒΡΫχΜθΦέΙΚΫχΝΥ“Μ≈ζ¬Χ…Ϊ ≥ΤΖΘ§»γΙϊ“‘30‘Σ/«ßΩΥœζ έ’β–©¬Χ…Ϊ ≥ΤΖΘ§Ρ«Ο¥ΟΩΧλΩ… έ≥ω400«ßΩΥΘ°”…œζ έΨ≠―ιΩ…÷ΣΘ§ΟΩΧλΒΡœζ έΝΩyΘ®«ßΩΥΘ©”κœζ έΒΞΦέxΘ®‘ΣΘ©Θ®xΓί30Θ©¥φ‘Ύ»γΆΦΥυ ΨΒΡ“Μ¥ΈΚ· ΐΙΊœΒΘ°
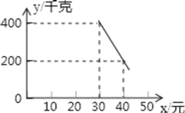
Θ®1Θ© ‘«σ≥ωy”κxΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®2Θ©…ηΗΟ≥§ –œζ έΗΟ¬Χ…Ϊ ≥ΤΖΟΩΧλΜώΒΟάϊ»σw‘ΣΘ§Β±œζ έΒΞΦέΈΣΚΈ÷Β ±Θ§ΟΩΧλΩ…ΜώΒΟΉν¥σάϊ»σΘΩΉν¥σάϊ»σ «Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΨΊ–Έ![]() ΒΡΕΞΒψ
ΒΡΕΞΒψ![]() Θ§
Θ§![]() Ζ÷±π‘Ύ
Ζ÷±π‘Ύ![]() ÷αΚΆ
÷αΚΆ![]() ÷α…œΘ§Βψ
÷α…œΘ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§ΥΪ«ζœΏ
Θ§ΥΪ«ζœΏ![]()
![]() ΒΡΆΦœσΨ≠Ιΐ
ΒΡΆΦœσΨ≠Ιΐ![]() ΒΡ÷–Βψ
ΒΡ÷–Βψ![]() Θ§«“”κ
Θ§«“”κ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ°
Θ°
Θ®1Θ©«σ![]() ΒΡ÷ΒΦΑΒψ
ΒΡ÷ΒΦΑΒψ![]() ΒΡΉχ±ξΘΜ
ΒΡΉχ±ξΘΜ
Θ®2Θ©»τΒψ![]() «
«![]() ±Ώ…œ“ΜΒψΘ§«“
±Ώ…œ“ΜΒψΘ§«“![]() œύΥΤ”Ύ
œύΥΤ”Ύ![]() Θ°«σ÷±œΏ
Θ°«σ÷±œΏ![]() ΒΡΫβΈω ΫΘ°
ΒΡΫβΈω ΫΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com