
【题目】如图,△ABC中,AB=AC,BE⊥AC于E,且D、E分别是AB、AC的中点.延长BC至点F,使CF=CE.

(1)求∠ABC的度数;
(2)求证:BE=FE;
(3)若AB=2,求△CEF的面积.
【答案】(1) ∠ABC=60°;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)根据等边三角形的判定得出△ABC是等边三角形,即可得出∠ABC的度数;
(2)根据BE=FE得出∠F=∠CEF=30°,再等边三角形的性质得出∠EBC=30°,即可证明;
(3)过E点作EG⊥BC,根据三角形面积解答即可.
试题解析:(1)∵BE⊥AC于E,E是AC的中点,
∴△ABC是等腰三角形,即AB=BC,
∵AB=AC,
∴△ABC是等边三角形,
∴∠ABC=60°;
(2)∵CF=CE,
∴∠F=∠CEF,
∵∠ACB=60°=∠F+∠CEF,
∴∠F=30°,
∵△ABC是等边三角形,BE⊥AC,
∴∠EBC=30°,
∴∠F=∠EBC,
∴BE=EF;
(3)过E点作EG⊥BC,如图:
∵BE⊥AC,∠EBC=30°,AB=BC=2,
∴BE=![]() ,CE=1=CF,
,CE=1=CF,
在△BEC中,EG=![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,O为数轴的原点,A,B为数轴上的两点,点A表示的数为-30,点B表示的数为100.
(1)A,B两点间的距离是________.
(2)若点C也是数轴上的点,点C到点B的距离是点C到原点O的距离的3倍,求点C表示的数.
(3)若电子蚂蚁P从点B出发,以6个单位长度/s的速度向左运动,同时另一只电子蚂蚁Q恰好从点A出发,以4个单位长度/s的速度向左运动,设两只电子蚂蚁同时运动到了数轴上的点D,那么点D表示的数是多少?
(4)若电子蚂蚁P从点B出发,以8个单位长度/s的速度向右运动,同时另一只电子蚂蚁Q恰好从点A出发,以4个单位长度/s的速度向右运动.设数轴上的点N到原点O的距离等于点P到原点O的距离的一半(点N在原点右侧),有下面两个结论:①ON+AQ的值不变;②ON-AQ的值不变,请判断哪个结论正确,并求出正确结论的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:
如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX=__________°;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=140°,∠BG1C=77°,求∠A的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
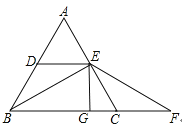
【题目】如图,已知O为直线AB上一点,过点O向直线AB上方引三条射线OC、OD、OE,且OC平分∠AOD,∠2=3∠1.
(1)若∠1=18°,求∠COE的度数;
(2)若∠COE=70°,求∠2的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,矩形ABCD中,BD=5cm,BC=4cm,E是边AD上一点,且BE = ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF + PG的长为( ).

A. 2.5 cm B. 2.8 cm C. 3 cm D. 3.5 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC、BD交于点O,BE平分∠ABC交AC于点F,交AD于点E,且∠DBF=15°,求证:(1)AO=AE; (2)∠FEO的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
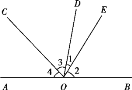
【题目】已知△ABC中,AB=AC=BC=6.点P射线BA上一点,点Q是AC的延长线上一点,且BP=CQ,连接PQ,与直线BC相交于点D.
(1)如图①,当点P为AB的中点时,求CD的长;
(2)如图②,过点P作直线BC的垂线,垂足为E,当点P,Q分别在射线BA和AC的延长线上任意地移动过程中,线段BE,DE,CD中是否存在长度保持不变的线段?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )
A.△CAE∽△BDA
B.![]()
C.BD?CE=4
D.BE=![]() BF
BF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com