
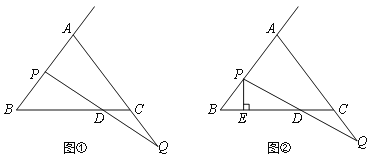
【题目】已知△ABC中,AB=AC=BC=6.点P射线BA上一点,点Q是AC的延长线上一点,且BP=CQ,连接PQ,与直线BC相交于点D.
(1)如图①,当点P为AB的中点时,求CD的长;
(2)如图②,过点P作直线BC的垂线,垂足为E,当点P,Q分别在射线BA和AC的延长线上任意地移动过程中,线段BE,DE,CD中是否存在长度保持不变的线段?请说明理由.
【答案】(1)CD=![]() ;(2)线段DE的长度保持不变,理由见解析.
;(2)线段DE的长度保持不变,理由见解析.
【解析】(1)过P点作PF∥AC交BC于F,即可构成小等边三角形BPF,再证明△PFD≌△QCD即可求解;
(2)根据(1)分两种情况:点P在线段AB上时,点P在BA的延长线上时分别求解即可得出结论.
解:(1)过P点作PF∥AC交BC于F,
∵点P为AB的中点,∴BP=![]() A B=3,
A B=3,
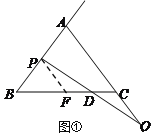
∵AB=AC=BC ,∴∠B=∠ACB=∠BAC=60°,
∵PF∥AC,∴∠PFB=∠ACB=60°,∠BPF=∠BAC=60°,
∴△PBF是等边三角形,
∴BF=FP=BP=3,∴FC=BC-BF=3,
由题意,BP=CQ,∴FP=CQ,
∵PF∥AC,∴∠DPF=∠DQC,
又∠PDF=∠QDC,∴△PFD≌△QCD,
∴CD=DF=![]() FC=
FC= ![]() ;
;
(2)当点P,Q在移动的过程中,线段DE的长度保持不变,
分两种情况讨论:
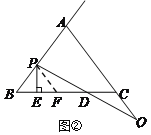
①当点P在线段AB上时,
过点P作PF∥AC交BC于F,由(1)知PB=PF,
∵PE⊥BC,∴BE=EF,
由(1)知△PFD≌△QCD,CD=DF,
∴DE=EF+DF=![]() BC=3,
BC=3,
②当点P在BA的延长线上时,同理可得DE=3,
∴当点P、Q在移动的过程中,线段DE的长度保持不变.


科目:初中数学 来源: 题型:
【题目】做如下操作:在等腰三角形ABC中,AB= AC,AD平分∠BAC,交BC于点D.将△ABD作关于直线AD的轴对称变换,所得的象与△ACD重合.
对于下列结论:①在同一个三角形中,等角对等边;②在同一个三角形中,等边对等角;
③等腰三角形的顶角平分线、底边上的中线和高互相重合.
由上述操作可得出的是 ▲ (将正确结论的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,BE⊥AC于E,且D、E分别是AB、AC的中点.延长BC至点F,使CF=CE.

(1)求∠ABC的度数;
(2)求证:BE=FE;
(3)若AB=2,求△CEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).
(1)求抛物线的解析式;
(2)D是y轴正半轴上的点,OD=3,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,
①试说明EF是圆的直径;
②判断△AEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
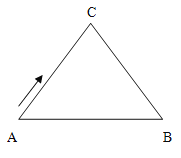
【题目】如图,△ABC中,AC=BC=10 cm,AB=12 cm,点D是AB的中点,连结CD,动点P从点A出发,沿A→C→B的路径运动,到达点B时运动停止,速度为每秒2 cm,设运动时间为![]() 秒.
秒.
(1)求CD的长;
(2)当![]() 为何值时,△ADP是直角三角形?
为何值时,△ADP是直角三角形?
(3)直接写出:当![]() 为何值时,△ADP是等腰三角形?
为何值时,△ADP是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中每个小正方形的顶点叫格点,△OAB的顶点的坐标分别为O(0,0)、A(1,3)、B(5,0).
(1)请画出与△OAB关于原点对称的△OCD;(其中A的对称点为C,B的对称点为D)
(2)在(1)的条件下,连接BC、DA,请画出一条直线MN(不与直线AC和坐标轴重合),将四边形ABCD的面积分成相等的两部分,其中M、N分别在AD和BC上,且M、N均为格点,并直接写出直线MN的解析式(写出一个即可).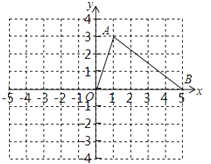
查看答案和解析>>
科目:初中数学 来源: 题型:
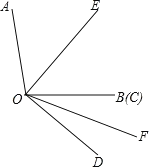
【题目】已知∠AOB=100°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.(本题中的角均为大于0°且小于等于180°的角).
(1)如图1,当OB、OC重合时,求∠EOF的度数;
(2)当∠COD从图1所示位置绕点O顺时针旋转n°(0<n<90)时,∠AOE﹣∠BOF的值是否为定值?若是定值,求出∠AOE﹣∠BOF的值;若不是,请说明理由.
(3)当∠COD从图1所示位置绕点O顺时针旋转n°(0<n<180)时,满足∠AOD+∠EOF=6∠COD,则n=__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com