
图1和图2中,优弧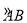 所在⊙O的半径为2,AB=2
所在⊙O的半径为2,AB=2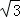 .点P为优弧
.点P为优弧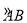 上一点(点P不与A,B重合),将图形沿BP折叠,得到点A的对称点A′.
上一点(点P不与A,B重合),将图形沿BP折叠,得到点A的对称点A′.
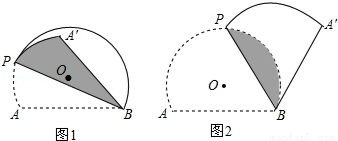
(1)点O到弦AB的距离是 ,当BP经过点O时,∠ABA′= °;
(2)当BA′与⊙O相切时,如图2,求折痕的长:
(3)若线段BA′与优弧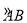 只有一个公共点B,设∠ABP=α.确定α的取值范围.
只有一个公共点B,设∠ABP=α.确定α的取值范围.
(1)1、60.(2)2 ;(3)α的取值范围是0°<α<30°或60°≤α<120°.
;(3)α的取值范围是0°<α<30°或60°≤α<120°.
【解析】
试题分析:(1)利用垂径定理和勾股定理即可求出点O到AB的距离;利用锐角三角函数的定义及轴对称性就可求出∠ABA′.
(2)根据切线的性质得到∠OBA′=90°,从而得到∠ABA′=120°,就可求出∠ABP,进而求出∠OBP=30°.过点O作OG⊥BP,垂足为G,容易求出OG、BG的长,根据垂径定理就可求出折痕的长.
(3)根据点A′的位置不同,分点A′在⊙O内和⊙O外两种情况进行讨论.点A′在⊙O内时,线段BA′与优弧 都只有一个公共点B,α的范围是0°<α<30°;当点A′在⊙O的外部时,从BA′与⊙O相切开始,以后线段BA′与优弧
都只有一个公共点B,α的范围是0°<α<30°;当点A′在⊙O的外部时,从BA′与⊙O相切开始,以后线段BA′与优弧 都只有一个公共点B,α的范围是60°≤α<120°.从而得到:线段BA′与优弧
都只有一个公共点B,α的范围是60°≤α<120°.从而得到:线段BA′与优弧 只有一个公共点B时,α的取值范围是0°<α<30°或60°≤α<120°.
只有一个公共点B时,α的取值范围是0°<α<30°或60°≤α<120°.
试题解析:(1)①过点O作OH⊥AB,垂足为H,连接OB,如图1①所示.
∵OH⊥AB,AB=2 ,
,
∴AH=BH= .
.
∵OB=2,
∴OH=1.
∴点O到AB的距离为1.
②当BP经过点O时,如图1②所示.
∵OH=1,OB=2,OH⊥AB,
∴sin∠OBH=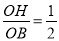 .
.
∴∠OBH=30°.
由折叠可得:∠A′BP=∠ABP=30°.
∴∠ABA′=60°.
(2)过点O作OG⊥BP,垂足为G,如图2所示.
∵BA′与⊙O相切,
∴OB⊥A′B.
∴∠OBA′=90°.
∵∠OBH=30°,
∴∠ABA′=120°.
∴∠A′BP=∠ABP=60°.
∴∠OBP=30°.
∴OG=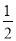 OB=1.
OB=1.
∴BG= .
.
∵OG⊥BP,
∴BG=PG= .
.
∴BP=2 .
.
∴折痕的长为2 .
.
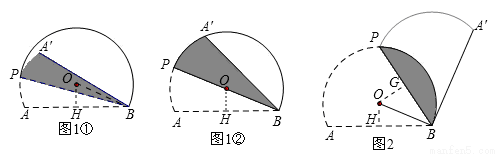
(3)若线段BA′与优弧 只有一个公共点B,
只有一个公共点B,
Ⅰ.当点A′在⊙O的内部时,此时α的范围是0°<α<30°.
Ⅱ.当点A′在⊙O的外部时,此时α的范围是60°≤α<120°.
综上所述:线段BA′与优弧 只有一个公共点B时,α的取值范围是0°<α<30°或60°≤α<120°.
只有一个公共点B时,α的取值范围是0°<α<30°或60°≤α<120°.
考点:圆的综合题.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源:2014-2015学年山东省新泰市九年级上学期学业水平模拟数学试卷(解析版) 题型:选择题
为了响应国家“发展低碳经济、走进低碳生活”的号召,到目前为止沈阳市共有60000户家庭建立了“低碳节能减排家庭档案”,则60000这个数用科学记数法表示为( )
A. 60×104 B. 6×105 C. 6×104 D. 0.6×106
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末调研数学试卷(解析版) 题型:解答题
(本小题满分10分)利达经销店为某工厂代销一种建筑材料.当每千克售价为260元时,月销售量为45千克.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每千克售价下降10元时,月销售量就会增加5千克.综合考虑各种因素,每售出一千克建筑材料共需支付厂家及其它费用100元.设每千克材料售价为x(元),该经销店的月利润为y(元).
(1)当每千克售价是240元时,计算此时的月销售量;
(2)求出y与x的函数关系式(不要求写出x的取值范围);
(3)该经销店要获得最大月利润,售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末调研数学试卷(解析版) 题型:选择题
二次函数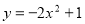 的图像上有两点P1(x1,y1),P2(x2,y2),当0<x1 <x2 时,
的图像上有两点P1(x1,y1),P2(x2,y2),当0<x1 <x2 时,
则y1 ,y2 的大小关系是( )
A.y1 >y2 B.y1< y2 <0 C.y1>y2> 0, D.y1<y2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末调研数学试卷(解析版) 题型:选择题
已知在Rt△ABC中,∠C=90°.若sinA=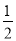 ,则cosA等于( ).
,则cosA等于( ).
A.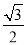 B.
B.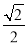 C.
C. D.1
D.1
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:解答题
如图,AB是⊙O的直径,弦CD⊥AB于点N,点M在⊙O上,∠1=∠C
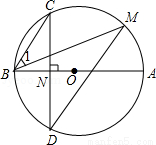
(1)求证:CB∥MD;
(2)若BC=4,sinM= ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:填空题
如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于 海里.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:选择题
在Rt△ABC中,∠C=90°,AB=6,cosB= ,则BC的长为( )
,则BC的长为( )
A.4 B.2 C.
C.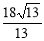 D.
D.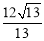
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省长汀县城区三校九年级12月联考数学试卷(解析版) 题型:解答题
(8分)如图,已知△ABC的三个顶点的坐标分别 为A(-6,0)、B(-2,3)、C(-1,0).(本题满分8分)
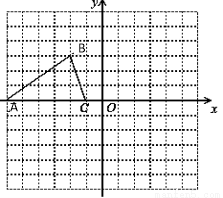
(1)将△ABC绕坐标原点O逆时针旋转90°.画出对应的△A′B′C′图形;
(2)若四边形A′B′C′D′为平行四边形,请直接写出第四个顶点D′的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com