
如图,AB是⊙O的直径,弦CD⊥AB于点N,点M在⊙O上,∠1=∠C
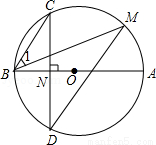
(1)求证:CB∥MD;
(2)若BC=4,sinM= ,求⊙O的直径.
,求⊙O的直径.
(1)证明见解析;(2)6.
【解析】
试题分析:(1)由∠C与∠M是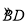 所对的圆周角,根据在同圆或等圆中,同弧或等弧所对的圆周角相等,即可得∠C=∠M,又由∠1=∠C,易得∠1=∠M,即可判定CB∥MD;
所对的圆周角,根据在同圆或等圆中,同弧或等弧所对的圆周角相等,即可得∠C=∠M,又由∠1=∠C,易得∠1=∠M,即可判定CB∥MD;
(2)首先连接AC,AB为⊙O的直径,可得∠ACB=90°,又由弦CD⊥AB,根据垂径定理的即可求得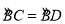 ,继而可得∠A=∠M,又由BC=4,sinM=
,继而可得∠A=∠M,又由BC=4,sinM=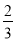 ,即可求得⊙O的直径.
,即可求得⊙O的直径.
试题解析:(1)证明:∵∠C与∠M是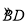 所对的圆周角,
所对的圆周角,
∴∠BCD=∠M,
又∵∠1=∠C,
∴∠1=∠M,
∴CB∥MD;
(2)【解析】
连接AC,

∵AB为⊙O的直径,
∴∠ACB=90°,
又∵CD⊥AB,
∴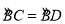
∴∠A=∠M,
∴sinA=sinM,
在Rt△ACB中,sinA=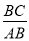 ,
,
∵sinM=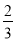 ,BC=4,
,BC=4,
∴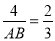
解得,AB=6,
即⊙O的直径为6.
考点:1.圆周角定理;2.垂径定理;3解直角三角形.


科目:初中数学 来源:2014-2015学年山东省滕州市九年级下学期学业水平模拟考试1数学试卷(解析版) 题型:解答题
(本小题满分12分)我们新定义一种三角形:两边平方和等于第三边平方的两倍的三角形叫做奇异三角形.
(1)根据“奇异三角形”的定义,请你判断命题“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A,B重合),D是半圆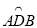 的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.

①求证:△ACE是奇异三角形;
②当△ACE是直角三角形时,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末调研数学试卷(解析版) 题型:解答题
(本小题满分6分)
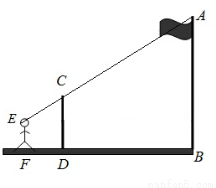
如图,九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度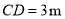 ,标杆与旗杆
,标杆与旗杆
的水平距离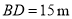 ,人的眼睛与地面的高度
,人的眼睛与地面的高度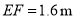 ,人与标杆
,人与标杆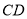 的水平距离
的水平距离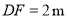 ,人的
,人的
眼睛E、标杆顶点C和旗杆顶点A在同一直线,求旗杆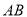 的高度.
的高度.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末调研数学试卷(解析版) 题型:选择题
如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )

A.P4 B.P3 C.P2 D.P1
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:解答题
图1和图2中,优弧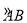 所在⊙O的半径为2,AB=2
所在⊙O的半径为2,AB=2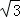 .点P为优弧
.点P为优弧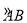 上一点(点P不与A,B重合),将图形沿BP折叠,得到点A的对称点A′.
上一点(点P不与A,B重合),将图形沿BP折叠,得到点A的对称点A′.
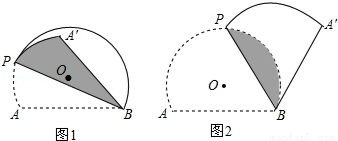
(1)点O到弦AB的距离是 ,当BP经过点O时,∠ABA′= °;
(2)当BA′与⊙O相切时,如图2,求折痕的长:
(3)若线段BA′与优弧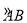 只有一个公共点B,设∠ABP=α.确定α的取值范围.
只有一个公共点B,设∠ABP=α.确定α的取值范围.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:填空题
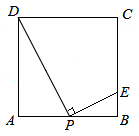
如图,在边长10cm为的正方形ABCD中,P为AB边上任意一点(P不与A、B两点重合),连结DP,过点P作PE⊥DP,垂足为P,交BC于点E,则BE的最大长度为 cm。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:填空题
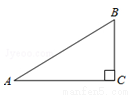
如图,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
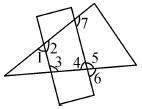
把一直尺放置在一个三角形纸片上,则下列结论正确的是( )
A.∠1+∠6>180° B.∠2+∠5<180° C.∠3+∠4<180° D.∠3+∠7>180°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省长汀县城区三校九年级12月联考数学试卷(解析版) 题型:填空题
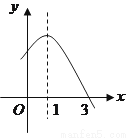
已知二次函数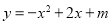 的部分图象如右图所示,则关于
的部分图象如右图所示,则关于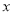 的一元二次方程
的一元二次方程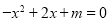 的解为__________。
的解为__________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com