
ΓΨΧβΡΩΓΩ“ΜΈΜΧ‘±ΠΒξ÷ςΉΦ±ΗΙΚΫχΦΉΓΔ““ΝΫ÷÷ΖΰΉΑΫχ––œζ έΘ§»τ“ΜΦΰΦΉ÷÷ΖΰΉΑΒΡΫχΦέ±»“ΜΦΰ““÷÷ΖΰΉΑΒΡΫχΦέΕύ![]() ‘ΣΘ§”Ο
‘ΣΘ§”Ο![]() ‘ΣΙΚΫχΦΉ÷÷ΖΰΉΑΒΡ ΐ «”Ο
‘ΣΙΚΫχΦΉ÷÷ΖΰΉΑΒΡ ΐ «”Ο![]() ‘ΣΙΚΫχ““÷÷ΖΰΉΑ ΐΒΡ
‘ΣΙΚΫχ““÷÷ΖΰΉΑ ΐΒΡ![]() ±ΕΘ°
±ΕΘ°
Θ®1Θ©«σΟΩΦΰΦΉ÷÷ΖΰΉΑΚΆ““÷÷ΖΰΉΑΒΡΫχΦέΖ÷±π «Εύ…Ό‘ΣΘΩ
Θ®2Θ©ΗΟΧ‘±ΠΒξΦΉ÷÷ΖΰΉΑΟΩΦΰ έΦέ![]() ‘ΣΘ§““÷÷ΖΰΉΑΟΩΦΰ έΦέ
‘ΣΘ§““÷÷ΖΰΉΑΟΩΦΰ έΦέ![]() ‘ΣΘ§Βξ÷ςΗυΨί¬ρΦ“–η«σΘ§ΨωΕ®œρ’βΦ“ΖΰΉΑ≥ßΙΚΫχ“Μ≈ζΖΰΉΑΘ§«“ΙΚΫχ““÷÷ΖΰΉΑΒΡ ΐ±»ΙΚΫχΦΉ÷÷ΖΰΉΑΒΡ ΐΒΡ
‘ΣΘ§Βξ÷ςΗυΨί¬ρΦ“–η«σΘ§ΨωΕ®œρ’βΦ“ΖΰΉΑ≥ßΙΚΫχ“Μ≈ζΖΰΉΑΘ§«“ΙΚΫχ““÷÷ΖΰΉΑΒΡ ΐ±»ΙΚΫχΦΉ÷÷ΖΰΉΑΒΡ ΐΒΡ![]() ±ΕΜΙΕύ
±ΕΜΙΕύ![]() ΦΰΘ§»τ±Ψ¥ΈΙΚΫχΒΡΝΫ÷÷ΖΰΉΑ»Ϊ≤Ω έ≥ωΚσΘ§Ήήάϊ»σΕύ”Ύ
ΦΰΘ§»τ±Ψ¥ΈΙΚΫχΒΡΝΫ÷÷ΖΰΉΑ»Ϊ≤Ω έ≥ωΚσΘ§Ήήάϊ»σΕύ”Ύ![]() ‘ΣΘ§«σΗΟΧ‘±ΠΒξ±Ψ¥ΈΙΚΫχΦΉ÷÷ΖΰΉΑ÷Ν…Ό «Εύ…ΌΦΰΘΩ
‘ΣΘ§«σΗΟΧ‘±ΠΒξ±Ψ¥ΈΙΚΫχΦΉ÷÷ΖΰΉΑ÷Ν…Ό «Εύ…ΌΦΰΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©ΟΩΦΰΦΉ÷÷ΖΰΉΑΒΡΫχΦέ «![]() ‘ΣΘ§ΟΩΦΰ““÷÷ΖΰΉΑΒΡΫχΦέ «
‘ΣΘ§ΟΩΦΰ““÷÷ΖΰΉΑΒΡΫχΦέ «![]() ‘ΣΘΜΘ®2Θ©ΗΟΧ‘±ΠΒξ±Ψ¥ΈΙΚΫχΦΉ÷÷ΖΰΉΑ÷Ν…Ό
‘ΣΘΜΘ®2Θ©ΗΟΧ‘±ΠΒξ±Ψ¥ΈΙΚΫχΦΉ÷÷ΖΰΉΑ÷Ν…Ό![]() ΦΰΘ°
ΦΰΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©…ηΟΩΦΰΦΉ÷÷ΖΰΉΑΈΣx‘ΣΘ§ΟΩΦΰ““÷÷ΖΰΉΑΈΣΘ®x-50Θ©‘ΣΘ§ΗυΨίΙΊΦϋ”οΨδΓΑ”Ο4000‘ΣΙΚΫχΦΉ÷÷ΖΰΉΑΒΡ ΐΝΩ «”Ο1500‘ΣΙΚΫχ““÷÷ΖΰΉΑΒΡ ΐΝΩΒΡ2±ΕΓ±Ω…Ν–ΖΫ≥Χ«σΫβΘΜ
Θ®2Θ©…ηΙΚΫχΦΉ÷÷ΖΰΉΑaΦΰΘ§‘ρΙΚΫχ““÷÷ΖΰΉΑΘ®2a+4Θ©ΦΰΘ§ΗυΨίΧβ“βΩ…ΒΟ≤ΜΒ»ΙΊœΒΘΚΦΉΖΰΉΑΒΡάϊ»σ+““ΖΰΉΑΒΡάϊ»σΘΨ7160‘ΣΘ§ΗυΨί≤ΜΒ»ΙΊœΒΝ–≥ω≤ΜΒ» ΫΘ§«σ≥ωΫβΦ·Θ§Φ¥Ω…»ΖΕ®¥πΑΗΘ°
ΫβΘΚΘ®1Θ©…ηΟΩΦΰΦΉ÷÷ΖΰΉΑΫχΦέ![]() ‘ΣΘ§ΟΩΦΰ““÷÷ΖΰΉΑΫχΦέ
‘ΣΘ§ΟΩΦΰ““÷÷ΖΰΉΑΫχΦέ![]() ‘ΣΘ§ΗυΨίΧβ“βΒΟΘ§
‘ΣΘ§ΗυΨίΧβ“βΒΟΘ§
![]() Θ§ΫβΒΟx=200Θ§
Θ§ΫβΒΟx=200Θ§
Ψ≠Φλ―ιx=200 «‘≠Ζ÷ ΫΖΫ≥ΧΒΡΫβΘ§
x-50=150Θ°
¥πΘΚΟΩΦΰΦΉ÷÷ΖΰΉΑΒΡΫχΦέ «![]() ‘ΣΘ§ΟΩΦΰ““÷÷ΖΰΉΑΒΡΫχΦέ «
‘ΣΘ§ΟΩΦΰ““÷÷ΖΰΉΑΒΡΫχΦέ «![]() ‘ΣΘ°
‘ΣΘ°
Θ®2Θ©…ηΗΟΧ‘±ΠΒξ±Ψ¥ΈΙΚΫχΦΉ÷÷ΖΰΉΑ![]() ΦΰΘ§‘ρΙΚΫχ““÷÷ΖΰΉΑΘ®2a+4Θ©ΦΰΘ§ΗυΨίΧβ“βΩ…ΒΟΘ§
ΦΰΘ§‘ρΙΚΫχ““÷÷ΖΰΉΑΘ®2a+4Θ©ΦΰΘ§ΗυΨίΧβ“βΩ…ΒΟΘ§
![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§
Θ§
![]() ΈΣ’ΐ’ϊ ΐΘ§
ΈΣ’ΐ’ϊ ΐΘ§![]() ΒΡΉν–Γ’ϊ ΐ÷ΒΈΣ
ΒΡΉν–Γ’ϊ ΐ÷ΒΈΣ![]() Θ°
Θ°
¥πΘΚΗΟΧ‘±ΠΒξ±Ψ¥ΈΙΚΫχΦΉ÷÷ΖΰΉΑ÷Ν…Ό![]() ΦΰΘ°
ΦΰΘ°


 »ΪΡήΝΖΩΦΨμœΒΝ–¥πΑΗ
»ΪΡήΝΖΩΦΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§2Ζ÷±π «Ρ≥ΩνάΚ«ρΦήΒΡ ΒΈοΆΦ”κ Ψ“βΆΦΘ§“―÷ΣΒΉΉυBC=0.60ΟΉΘ§ΒΉΉυBC”κ÷ßΦήACΥυ≥…ΒΡΫ«ΓœACB=75ΓψΘ§÷ßΦήAFΒΡ≥ΛΈΣ2.50ΟΉΘ§άΚΑεΕΞΕΥFΒψΒΫάΚΩρDΒΡΨύάκFD=1.35ΟΉΘ§άΚΑεΒΉ≤Ω÷ßΦήHE”κ÷ßΦήAFΥυ≥…ΒΡΫ«ΓœFHE=60ΓψΘ§«σάΚΩρDΒΫΒΊΟφΒΡΨύάκΘ®ΨΪ»ΖΒΫ0.01ΟΉΘ©Θ®≤ΈΩΦ ΐΨίΘΚcos75ΓψΓ÷0.2588Θ§sin75ΓψΓ÷0.9659Θ§tan75ΓψΓ÷3.732Θ§![]() Γ÷1.732Θ§
Γ÷1.732Θ§![]() Γ÷1.414Θ©
Γ÷1.414Θ©

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§AD «BC±Ώ…œΒΡΗΏΘ§E «ACΒΡ÷–ΒψΘ§P «AD…œΒΡ“ΜΗωΕ·ΒψΘ§Β±PC”κPEΒΡΚΆΉν–Γ ±Θ§ΓœCPEΒΡΕ» ΐ «Θ® Θ©
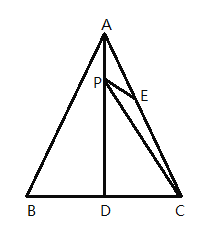
A.30ΓψB.45ΓψC.60ΓψD.90Γψ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΘ§Γ―OΈΣΓςABCΒΡΆβΫ”‘≤Θ§BCΈΣ÷±ΨΕΘ§ΒψE‘ΎAB…œΘ§ΙΐΒψEΉςEFΓΆBCΘ§ΒψG‘ΎFEΒΡ―”≥ΛœΏ…œΘ§«“GA=GEΘ°
Θ®1Θ©«σ÷ΛΘΚAG”κΓ―Oœύ«–Θ°
Θ®2Θ©»τAC=6Θ§AB=8Θ§BE=3Θ§«σœΏΕΈOEΒΡ≥ΛΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΙΪΥΨ“ΣΙΚ¬ρ“Μ÷÷± Φ«±ΨΙ©‘±ΙΛ―ßœΑ ± Ι”Ο.‘ΎΦΉΈΡΨΏΒξ≤ΜΙή“Μ¥ΈΙΚ¬ρΕύ…Ό±ΨΘ§ΟΩ±ΨΦέΗώΈΣ2‘Σ.‘Ύ““ΈΡΨΏΒξΙΚ¬ρΆ§―υΒΡ± Φ«±ΨΘ§“Μ¥ΈΙΚ¬ρ ΐΝΩ≤Μ≥§Ιΐ20 ±Θ§ΟΩ±ΨΦέΗώΈΣ2.4‘ΣΘΜ“Μ¥ΈΙΚ¬ρ ΐΝΩ≥§Ιΐ20 ±Θ§≥§Ιΐ≤ΩΖ÷ΟΩ±ΨΦέΗώΈΣ1.8‘Σ.
…η‘ΎΆ§“ΜΦ“ΈΡΨΏΒξ“Μ¥ΈΙΚ¬ρ’β÷÷± Φ«±ΨΒΡ ΐΝΩΈΣx(xΈΣΖ«ΗΚ’ϊ ΐ).
(Δώ)ΗυΨίΧβ“βΘ§Χν–¥œ¬±μΘΚ
“Μ¥ΈΙΚ¬ρ ΐΝΩ(±Ψ) | 10 | 20 | 30 | 40 | Γ≠ |
ΦΉΈΡΨΏΒξΗΕΩνΫπΕν(‘Σ) | 20 | 60 | Γ≠ | ||
““ΈΡΨΏΒξΗΕΩνΫπΕν(‘Σ) | 24 | 66 | Γ≠ |
(Δρ)…η‘ΎΦΉΈΡΨΏΒξΙΚ¬ρ’β÷÷± Φ«±ΨΒΡΗΕΩνΫπΕνΈΣ![]() ‘ΣΘ§‘Ύ““ΈΡΨΏΒξΙΚ¬ρ’β÷÷± Φ«±ΨΒΡΗΕΩνΫπΕνΈΣ
‘ΣΘ§‘Ύ““ΈΡΨΏΒξΙΚ¬ρ’β÷÷± Φ«±ΨΒΡΗΕΩνΫπΕνΈΣ![]() ‘ΣΘ§Ζ÷±π–¥≥ω
‘ΣΘ§Ζ÷±π–¥≥ω![]() Θ§
Θ§![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΚ· ΐΙΊœΒ ΫΘΜ
ΒΡΚ· ΐΙΊœΒ ΫΘΜ
(Δσ)Β±![]() ±Θ§‘ΎΡΡΦ“ΈΡΨΏΒξΙΚ¬ρ’β÷÷± Φ«±ΨΒΡΜ®Ζ―…ΌΘΩ«κΥΒΟςάμ”….
±Θ§‘ΎΡΡΦ“ΈΡΨΏΒξΙΚ¬ρ’β÷÷± Φ«±ΨΒΡΜ®Ζ―…ΌΘΩ«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΫώΡξΈ“ –ΫΪ¥¥Ϋ®»ΪΙζ…≠Ν÷≥« –Θ§Χα≥ωΝΥΓΑΙ≤Ϋ®¬Χ…Ϊ≥«Γ±ΒΡ≥Ϊ“ιΘ°Ρ≥–ΘΜΐΦΪœλ”ΠΘ§‘Ύ3‘¬12»’÷≤ ςΫΎ’βΧλΉι÷·»Ϊ–Θ―ß…ζΩΣ’ΙΝΥ÷≤ ςΜνΕ·Θ§–ΘΆ≈Έ·Ε‘»Ϊ–ΘΗςΑύΒΡ÷≤ ς«ιΩωΒά––ΝΥΆ≥ΦΤΘ§Μφ÷ΤΝΥ»γΆΦΥυ ΨΒΡΝΫΗω≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ°
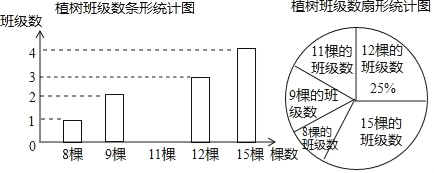
Θ®1Θ©«σΗΟ–ΘΒΡΑύΦΕΉή ΐΘΜ
Θ®2Θ©ΫΪΧθ–ΈΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
Θ®3Θ©«σΗΟ–ΘΗςΑύ‘Ύ’β“ΜΜνΕ·÷–÷≤ ςΒΡΤΫΨυ ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() «
«![]() ΒΡΤΫΖ÷œΏΘ§Ψ≠Ιΐ
ΒΡΤΫΖ÷œΏΘ§Ψ≠Ιΐ![]() Θ§
Θ§![]() ΝΫΒψΒΡ‘≤ΒΡ‘≤–Ρ
ΝΫΒψΒΡ‘≤ΒΡ‘≤–Ρ![]() «ΓΚΟ¬δ‘Ύ
«ΓΚΟ¬δ‘Ύ![]() …œΘ§
…œΘ§![]() Ζ÷±π”κ
Ζ÷±π”κ![]() ΓΔ
ΓΔ![]() œύΫΜ”ΎΒψ
œύΫΜ”ΎΒψ![]() ΓΔ
ΓΔ![]() Θ°»τ‘≤ΑκΨΕΈΣ2Θ°‘ρ“θ”Α≤ΩΖ÷ΟφΜΐΘ® Θ©Θ°
Θ°»τ‘≤ΑκΨΕΈΣ2Θ°‘ρ“θ”Α≤ΩΖ÷ΟφΜΐΘ® Θ©Θ°
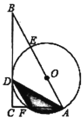
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏΕΞΒψAΒΡΉχ±ξΈΣΘ®1Θ§4Θ©Θ§≈ΉΈοœΏ”κx÷αœύΫΜ”ΎBΓΔCΝΫΒψΘ§”κy÷αΫΜ”ΎΒψEΘ®0Θ§3Θ©Θ°
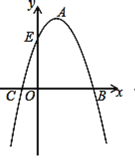
Θ®1Θ©«σ≈ΉΈοœΏΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©“―÷ΣΒψFΘ®0Θ§©¹3Θ©Θ§‘Ύ≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œ «Ζώ¥φ‘Ύ“ΜΒψGΘ§ ΙΒΟEG+FGΉν–ΓΘ§»γΙϊ¥φ‘ΎΘ§«σ≥ωΒψGΒΡΉχ±ξΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒΡΎΘ§≈ΉΈοœΏ![]() ”κx÷αΫΜ”ΎΒψAΘ§CΘ®ΒψA‘ΎΒψCΒΡΉσ≤ύΘ©Θ§”κy÷αΫΜ”ΎΒψBΘ§ΕΞΒψΈΣD.ΒψQΈΣœΏΕΈBCΒΡ»ΐΒ»Ζ÷ΒψΘ®ΩΩΫϋΒψCΘ©.
”κx÷αΫΜ”ΎΒψAΘ§CΘ®ΒψA‘ΎΒψCΒΡΉσ≤ύΘ©Θ§”κy÷αΫΜ”ΎΒψBΘ§ΕΞΒψΈΣD.ΒψQΈΣœΏΕΈBCΒΡ»ΐΒ»Ζ÷ΒψΘ®ΩΩΫϋΒψCΘ©.
Θ®1Θ©ΒψMΈΣ≈ΉΈοœΏΕ‘≥Τ÷α…œ“ΜΒψΘ§ΒψEΈΣΕ‘≥Τ÷α”“≤ύ≈ΉΈοœΏ…œΒΡΒψ«“ΈΜ”ΎΒΎ“ΜœσœόΘ§Β±![]() ΒΡ÷ή≥ΛΉν–Γ ±Θ§«σ
ΒΡ÷ή≥ΛΉν–Γ ±Θ§«σ![]() ΟφΜΐΒΡΉν¥σ÷ΒΘΜ
ΟφΜΐΒΡΉν¥σ÷ΒΘΜ
Θ®2Θ©‘ΎΘ®1Θ©ΒΡΧθΦΰœ¬Θ§Β±![]() ΒΡΟφΜΐΉν¥σ ±Θ§ΙΐΒψEΉς
ΒΡΟφΜΐΉν¥σ ±Θ§ΙΐΒψEΉς![]() ÷αΘ§¥ΙΉψΈΣNΘ§ΫΪœΏΕΈCN»ΤΒψCΥ≥ ±’κ–ΐΉΣ90ΓψΒΟΒΫΒψNΘ§‘ΌΫΪΒψNœρ…œΤΫ“Τ
÷αΘ§¥ΙΉψΈΣNΘ§ΫΪœΏΕΈCN»ΤΒψCΥ≥ ±’κ–ΐΉΣ90ΓψΒΟΒΫΒψNΘ§‘ΌΫΪΒψNœρ…œΤΫ“Τ![]() ΗωΒΞΈΜ≥ΛΕ».ΒΟΒΫΒψPΘ§ΒψG‘Ύ≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œΘ§«κΈ ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒΡΎ «Ζώ¥φ‘Ύ“ΜΒψHΘ§ ΙΒψDΘ§PΘ§GΘ§HΙΙ≥…Νβ–Έ.»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΒψHΒΡΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΗωΒΞΈΜ≥ΛΕ».ΒΟΒΫΒψPΘ§ΒψG‘Ύ≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œΘ§«κΈ ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒΡΎ «Ζώ¥φ‘Ύ“ΜΒψHΘ§ ΙΒψDΘ§PΘ§GΘ§HΙΙ≥…Νβ–Έ.»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΒψHΒΡΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com