
����Ŀ����1����ͼ1��A��a��0����B��b��0����a��b����|a+4|+![]() =0
=0
����a��b��ֵ��
����C����6��0������CB����BE��CB������ΪB����BC=BE����AE��y����P����P�����ꣻ
��2����ͼ2����A��6��0����B��0��3������Q��A��������ÿ��1����λ���ٶ�������AO�����˶������Q�˶�ʱ��Ϊt�룬��Q����ֱ��AB�Ĵ��ߣ�����ΪD��ֱ��QD��y�ύ��E�㣬�ڵ�Q���˶������У�һ��������EOQ�ա�AOB����ֱ��д�����ڵ�tֵ�Լ���Ӧ��E�����꣮
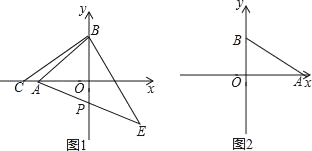
���𰸡���1����a=-4��b=4������E����y�ᴹ���ɣ�P��0��-2������2�������������t=3ʱ����EΪ��0��-6������t=9ʱ����EΪ��0��6����
��������
���⣨1�����⿼��������ȫ�ȵ��ж���������Ŀ�е���Ϣ�����Ӧ�ĵ�����꣬���Ը�����Ŀ�е���Ϣ������Ӧ��ͼ�Σ��ؼ�����ȷ������Ŀ�е���Ϣ�������Ҫ��Ľ��ۣ�����a��b����![]() ���������a��b��ֵ������EF��y���ڵ�F��������Ŀ�е���Ϣ�������Ƴ���BCO�ա�EBF��Ȼ����ݶ�Ӧ��ϵ�����Ӧ�ߵij��ȣ��Ӷ�������õ�P�����꣮��2������������Ի�����Ӧ��ͼ�Ӷ�����ֱ��д��t��ֵ����Ӧ�ĵ�E��ֵ��
���������a��b��ֵ������EF��y���ڵ�F��������Ŀ�е���Ϣ�������Ƴ���BCO�ա�EBF��Ȼ����ݶ�Ӧ��ϵ�����Ӧ�ߵij��ȣ��Ӷ�������õ�P�����꣮��2������������Ի�����Ӧ��ͼ�Ӷ�����ֱ��д��t��ֵ����Ӧ�ĵ�E��ֵ��
�����������1���١�a��b����|a+4|+![]() =0�� ��a+4=0��a+b=0�� ��ã�a=-4��b=4��
=0�� ��a+4=0��a+b=0�� ��ã�a=-4��b=4��
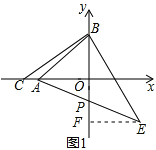
����ͼ��ʾ����EF��y���ڵ�F�� ����EFB=90���� ��BE��CB������ΪB����BC=BE����BOC=90����
���COB=��EFB����CBO=��BEF�� ���BCO�ա�EBF�� ��A��-4��0��B��4��0����C��-6��0����
��EF=OB=4��BF=OC=6�� ����E��������4��-2���� ��A��-4��0����
�����A��E�Ľ���ʽΪ��y=kx+b��
��![]() �� ��ã�k��
�� ��ã�k��![]() ��b��1�� ��y��
��b��1�� ��y��![]() x1��
x1��
��x=0����y=-1�� �ʵ�P������Ϊ��0��-1����
��2���������⣬�����������
��һ�������ͼ��ʾ��
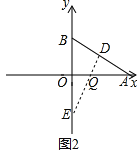
��A��6��0����B��0��3������EOQ�ա�AOB�� ��OQ=OB��OE=OA��
��AQ=3����E������Ϊ��0��-6���� ����Q��A��������ÿ��1����λ���ٶ�������AO�����˶���
����Q�˶���ʱ��t=3�룮 �ʴ�ʱt��ֵΪ3����E������Ϊ��0��-6����
�ڶ����������ͼ��ʾ��
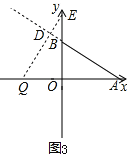
��A��6��0����B��0��3������EOQ�ա�AOB�� ��OQ=OB��OE=OA��
��AQ=9����E������Ϊ��0��6���� ����Q��A��������ÿ��1����λ���ٶ�������AO�����˶���
����Q�˶���ʱ��t=9�룮 �ʴ�ʱt��ֵΪ9����E������Ϊ��0��6����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
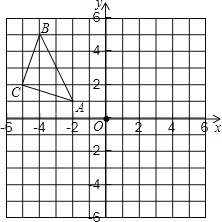
����Ŀ������̽������ͼ����ABC��ƽ��ֱ������ϵ�У����У���A��B��C������ֱ�ΪA���C2��1����B���C4��5����C���C5��2����
��1������ABC����ֱ��l��x=�C1�ԳƵ���A1B1C1�����У���A�� B��C�ĶԳƵ�ֱ�Ϊ��A1��B1��C1��
��2�����C1������__________��
��3����ƽ��ֱ������ϵ����һ��Pλ�ڵ������ޣ��������ʾΪP��m��n�������P����ֱ��l�ĶԳƵ�Q�������ʾΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڱ߳�Ϊ1��С�����������У���AOB�Ķ�����ڸ���ϣ�

��1��B�����y��ĶԳƵ�����Ϊ ��
��2������AOB����ƽ��3����λ���ȣ�������ƽ��2����λ���ȵõ���A1O1B1���뻭����A1O1B1��
��3���ڣ�2���������£���AOB��AB����һ��P������Ϊ��a��b������ƽ�ƺ��Ӧ��P1������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AC=6��BC=8����F�ڱ�AC�ϣ�����CF=2����EΪ��BC�ϵĶ��㣬����CEF��ֱ��EF���ۣ���C���ڵ�P�������P����AB�������Сֵ�� �� 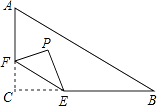
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
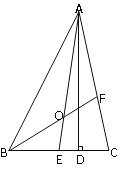
����Ŀ����ͼ����ABC�У�AD�Ǹߣ�AE��BF�ǽ�ƽ���ߣ������ཻ�ڵ�O����BAC=50�㣬��C=70�������DAC����BOA�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��б��AB���¶���i=1��2���½�B����һ����BC��ijһʱ�̲����BC��б��AB�ϵ�Ӱ��BD�ij�����10�ף���ʱ���̫��������ˮƽ�ߵļн�Ϊ60�㣬����BC�ĸ߶�Ϊ�����ף�������������ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=��x+3��x�ᣬy��ֱ���B��C���㣬������y=ax2+bx+c��A��1��0����B��C���㣮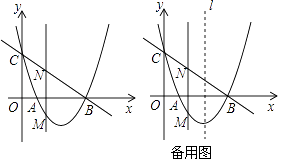
��1���������ߵĽ���ʽ��
��2������M����������x���·�ͼ���ϵĶ��㣬����M��MN��y�ύֱ��BC�ڵ�N�����߶�MN�����ֵ��
��3���ڣ�2���������£���MNȡ�����ֵʱ���������ߵĶԳ���l���Ƿ���ڵ�P��ʹ��PBN����BNΪ���ĵ��������Σ������ڣ������P�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������˾�Ŀ�ݳ��ͻ���ͬʱ�Ӽس������Ը��Ե��ٶ��������ҵ���ʻ����ݳ������ҵغ�������Ʒ����װ���ﹲ��45���ӣ�������ԭ·����һ�ٶ����ٷ��أ�ֱ���������������֪�������ٶ�Ϊ60ǧ��/ʱ������֮��ľ���y��ǧ�ף��������ʻʱ��x��Сʱ��֮��ĺ���ͼ����ͼ��ʾ����������4�����ۣ� �ٿ�ݳ��Ӽص��ҵص��ٶ�Ϊ100ǧ��/ʱ��
�ڼס�������֮��ľ���Ϊ120ǧ�ף�
��ͼ�е�B������Ϊ��3 ![]() ��75����
��75����
�ܿ�ݳ����ҵط���ʱ���ٶ�Ϊ90ǧ��/ʱ��
����4��������ȷ���� �� 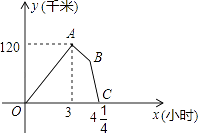
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ1����ABC�DZ߳�Ϊ4�ĵȱ������Σ���O�ڱ�AB�ϣ���O����B�ҷֱ����AB��BC�ཻ�ڵ�D��E��EF��AC������ΪF�� 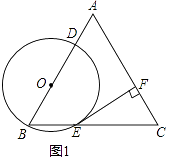
��1����֤��ֱ��EF�ǡ�O�����ߣ�
��2����ͼ2����ֱ��AC���O����ʱ�����O�İ뾶�� 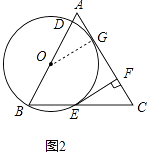
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com