
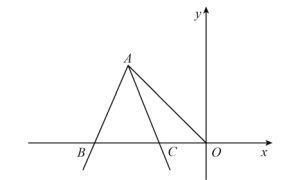
����Ŀ��ij������˾�Ŀ�ݳ��ͻ���ͬʱ�Ӽس������Ը��Ե��ٶ��������ҵ���ʻ����ݳ������ҵغ�������Ʒ����װ���ﹲ��45���ӣ�������ԭ·����һ�ٶ����ٷ��أ�ֱ���������������֪�������ٶ�Ϊ60ǧ��/ʱ������֮��ľ���y��ǧ�ף��������ʻʱ��x��Сʱ��֮��ĺ���ͼ����ͼ��ʾ����������4�����ۣ� �ٿ�ݳ��Ӽص��ҵص��ٶ�Ϊ100ǧ��/ʱ��
�ڼס�������֮��ľ���Ϊ120ǧ�ף�
��ͼ�е�B������Ϊ��3 ![]() ��75����
��75����
�ܿ�ݳ����ҵط���ʱ���ٶ�Ϊ90ǧ��/ʱ��
����4��������ȷ���� �� 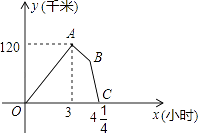
���𰸡��٢ۢ�
���������⣺�����ݳ��Ӽص��ҵص��ٶ�Ϊxǧ��/ʱ���� 3��x��60��=120��
x=100�����ʢ���ȷ����
����Ϊ120ǧ���ǿ�ݳ������ҵغ�����֮��ľ��룬���Ǽס�������֮��ľ��룬���ʢڴ���
����Ϊ��ݳ������ҵغ�������Ʒ����װ���ﹲ��45���ӣ�
����ͼ�е�B�ĺ�����Ϊ3+ ![]() =3
=3 ![]() ��
��
������Ϊ120��60�� ![]() =75�����ʢ���ȷ����
=75�����ʢ���ȷ����
�����ݳ����ҵط���ʱ���ٶ�Ϊyǧ��/ʱ����
��y+60����4 ![]() ��3
��3 ![]() ��=75��
��=75��
y=90�����ʢ���ȷ����
�ʴ�Ϊ���٢ۢܣ�
����һ�κ��������ʺ�ͼ����ʵ�������ÿһ����з������ɵó��𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������и���
��1��������ֵ����1�� ![]() ����
���� ![]() ������ϲ������������ֵ��
������ϲ������������ֵ��
��2�����㣺|1�� ![]() |��2sin45��+���Щ�3.14��0+2��2 ��
|��2sin45��+����3.14��0+2��2 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
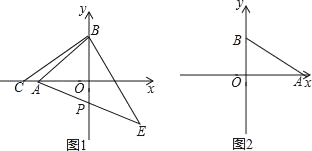
����Ŀ����1����ͼ1��A��a��0����B��b��0����a��b����|a+4|+![]() =0
=0
����a��b��ֵ��
����C����6��0������CB����BE��CB������ΪB����BC=BE����AE��y����P����P�����ꣻ
��2����ͼ2����A��6��0����B��0��3������Q��A��������ÿ��1����λ���ٶ�������AO�����˶������Q�˶�ʱ��Ϊt�룬��Q����ֱ��AB�Ĵ��ߣ�����ΪD��ֱ��QD��y�ύ��E�㣬�ڵ�Q���˶������У�һ��������EOQ�ա�AOB����ֱ��д�����ڵ�tֵ�Լ���Ӧ��E�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������A1B1C1O��A2B2C2C1 �� A3B3C3C2 �� ������ͼ��ʾ���ã���A1 �� A2 �� A3 �� �͵�C1 �� C2 �� C3 �� �����ֱ���ֱ��y=kx+b��k��0����x���ϣ���֪��B1 �� B2 �� B3 �� B4������ֱ�Ϊ��1��1����3��2������7��4������15��8������Bn�������ǣ� �� 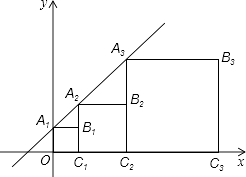
A.��2n��1��2n��1��
B.��2n �� 2n��1��
C.��2n��1 �� 2n��
D.��2n��1��1��2n��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵȱ���ABC��������AD��ʹ��AD��AC��ֱ��AB�����࣬��BAD=����0�㣼����180��������B����ֱ��AD�ĶԳƵ�ΪP������PB��PC��
��1�������ⲹȫͼ1��
��2����ͼ1�У�����BPC�Ķ�����
��3��ֱ��д��ʹ����PBC�ǵ��������ε�����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڱ߳�Ϊ1��С�����������У���AOB�Ķ�����ڸ���ϣ�
��1��B�����y��ĶԳƵ�����Ϊ ��
��2������AOB����ƽ��3����λ���ȵõ���A1O1B1���뻭����A1O1B1��
��3���ڣ�2���������£�A1������Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���й���һ���ľߴ���ÿ������Ϊ10Ԫ���������ڼ䣬��¼��ÿ����������������۵��۵��������±���
���۵���x��Ԫ | 11 | 12 | 13 | 14 | 15 | �� |
��������y������ | 38 | 36 | 34 | 32 | 30 | �� |
��ע����۾ֹ涨��ÿ���ľߴ����ۼ۲�����10Ԫ�Ҳ�����18Ԫ | ||||||
������ݱ�����Ϣ����������⣺
��1��y��x���������亯����ϵʽΪ
��2��ӪҵԱ������һ���������150Ԫ�������۵���ΪԪ��
��3�������۵�Ŀ������Ҫÿ��������������������������۾�������һ�£�����������µ���x��Ԫ��Ӧ��Ϊ����ʱ��ÿ�����������w��Ԫ�������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
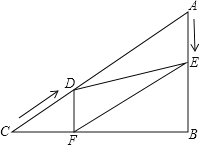
����Ŀ����ͼ��ʾ����Rt��ABC�У���B=90�㣬AC=100cm����A=60������D�ӵ�C������CA������4cm/s���ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������2cm/s���ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t�루0��t��25��������D��DF��BC�ڵ�F������DE��EF��
��1����֤���ı���AEFD��ƽ���ı��Σ�
��2���ı���AEFD�ܹ���Ϊ����������ܣ������Ӧ��tֵ��������ܣ���˵�����ɣ�
��3����tΪ��ֵʱ����DEFΪֱ�������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
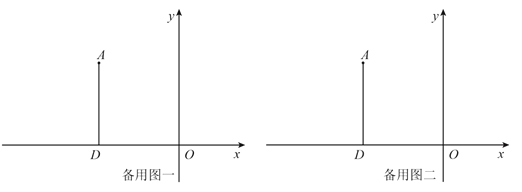
����Ŀ����ƽ��ֱ������ϵ�У��� ![]() ������Ϊ
������Ϊ![]() ���� A Ϊ�����
���� A Ϊ�����![]() ������ʼ����
������ʼ���� ![]() �ύ��
�ύ�� ![]() ��
��![]() ���㣨
���㣨![]() ��
�� ![]() ���棩����
���棩����![]() ��
��
��1����ͼ������![]() ����
���� ![]() ʱ����˵����
ʱ����˵����![]() ��
��
��2������ ![]() ��
��![]() �ᣬ����Ϊ
�ᣬ����Ϊ![]() ����
����![]() ʱ����
ʱ����![]() ��
��![]() ����ֱ�߷��ۣ����ۺ��
����ֱ�߷��ۣ����ۺ��![]() ��
�� ![]() ���ڵ�
���ڵ� ![]() �����
����� ![]() ������.
������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com