
【题目】在平面直角坐标系中,点 ![]() 的坐标为
的坐标为![]() ,以 A 为顶点的
,以 A 为顶点的![]() 的两边始终与
的两边始终与 ![]() 轴交于
轴交于 ![]() 、
、![]() 两点(
两点(![]() 在
在 ![]() 左面),且
左面),且![]() .
.
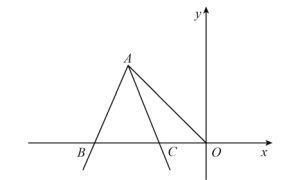
(1)如图,连接![]() ,当
,当 ![]() 时,试说明:
时,试说明:![]() .
.
(2)过点 ![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,当
,当![]() 时,将
时,将![]() 沿
沿![]() 所在直线翻折,翻折后边
所在直线翻折,翻折后边![]() 交
交 ![]() 轴于点
轴于点 ![]() ,求点
,求点 ![]() 的坐标.
的坐标.
【答案】(1)见解析;(2)M点坐标为(0,3)或M点坐标为(0,—6).
【解析】
试题(1)根据题目中角的度数,求出∠BAO=∠ABC=67.5°,利用等腰三角形的性质即可得出结论;
(2)根据题意,可知要分两种情况,即当点C在点D右侧时或当点C在点D左侧时,利用勾股定理即可得出M点坐标.
试题解析:
(1)∵AB=AC,∠BAC=45°,∴∠ABC=∠ACB= 67.5°.
过点A作AE⊥OB于E,则△AEO是等腰直角三角形,∠EAO=45°.
∵AB=AC,AE⊥OB,
∴∠BAE=![]() ∠BAC=22.5°.
∠BAC=22.5°.
∴∠BAO=67.5°=∠ABC
∴OA=OB,
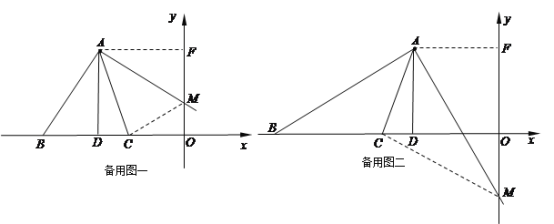
(2)设OM=x.
当点C在点D右侧时,连接CM,过点A作AF⊥y轴于点F,
由∠BAM=∠DAF=90°可知:∠BAD=∠MAF;
∵AD=AF=6,∠BDA=∠MFA=90°,
∴△BAD≌△MAF.
∴BD=FM=6—x.
∵AC=AC,∠BAC=∠MAC,
∴△BAC≌△MAC.
∴BC=CM=8—x.
在Rt△COM中,由勾股定理得:OC2+OM2=CM2,即![]() ,
,
解得:x=3,∴M点坐标为(0,3).
当点C在点D左侧时,连接CM,过点A作AF⊥y轴于点F,
同理,△BAD≌△MAF,∴BD=FM=6+x.
同理,△BAC≌△MAC,∴BC=CM=4+x.
在Rt△COM中,由勾股定理得:OC2+OM2=CM2,即![]() ,
,
解得:x=6,∴M点坐标为(0,—6)


科目:初中数学 来源: 题型:
【题目】某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论: ①快递车从甲地到乙地的速度为100千米/时;
②甲、乙两地之间的距离为120千米;
③图中点B的坐标为(3 ![]() ,75);
,75);
④快递车从乙地返回时的速度为90千米/时,
以上4个结论正确的是 . 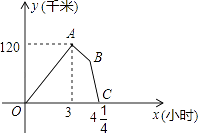
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F. 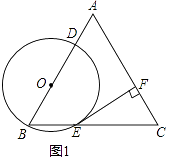
(1)求证:直线EF是⊙O的切线;
(2)如图2,当直线AC与⊙O相切时,求⊙O的半径. 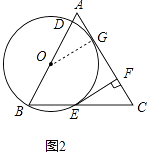
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD为正方形,AB=2 ![]() ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由;
(3)设AE=x,四边形DEFG的面积为S,求出S与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将△ABC沿着某一方向平移一定的距离得到△MNL,则下列结论中正确的有( )
①AM∥BN;②AM=BN;③BC=ML;④∠ACB=∠MNL。
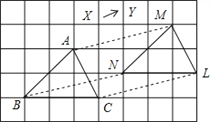
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30o,点A1、A2、A3 在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7 的边长为【 】

A.6 B.12 C.32 D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,我市组织了一次初三年级1200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
成绩(分) | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |
成绩分组 | 频数 | 频率 |
35≤x<38 | 3 | 0.03 |
38≤x<41 | a | 0.12 |
41≤x<44 | 20 | 0.20 |
44≤x<47 | 35 | 0.35 |
47≤x≤50 | 30 | b |
请根据所提供的信息解答下列问题:
(1)样本的中位数是分;
(2)频率统计表中a= , b=;
(3)请补全频数分布直方图;
(4)请根据抽样统计结果,估计该次大赛中成绩不低于41分的学生有多少人? 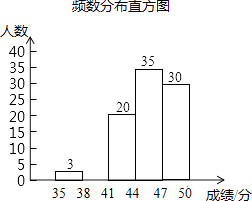
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三角形的第一条边的长是![]() ,第二条边长是第一条边长的2倍少3,第三条边比第二条边短5。
,第二条边长是第一条边长的2倍少3,第三条边比第二条边短5。
(1)用含![]() 、
、![]() 的式子表示这个三角形的周长;
的式子表示这个三角形的周长;
(2)当![]() ,
,![]() 时,求这个三角形的周长;
时,求这个三角形的周长;
(3)当![]() ,三角形的周长为 39时,求各边长。
,三角形的周长为 39时,求各边长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的5个小球,其中红球3个,黑球2个.
(1)先从袋中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:若A为必然事件,则m的值为 , 若A为随机事件,则m的取值为;
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,求这个事件的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com