
【题目】如图所示,将△ABC沿着某一方向平移一定的距离得到△MNL,则下列结论中正确的有( )
①AM∥BN;②AM=BN;③BC=ML;④∠ACB=∠MNL。
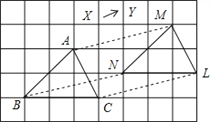
A. 1个 B. 2个 C. 3个 D. 4个
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.

(1)请画出平移后的△A′B′C′,并求△A′B′C′的面积;
(2)若连接AA′,CC′,则这两条线段之间的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过15吨(含15吨)时,每吨按政府补贴优惠价收费;每月超过15吨时,超过部分每吨按市场调节价收费.小明家1月份用水23吨,交水费35元,2月份用水19吨,交水费25元.
(1)求每吨水的政府补贴优惠价与市场调节价分别是多少;
(2)小明家3月份用水24吨,他家应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线C:y=x2经过变化可得到抛物线C1:y1=a1x(x﹣b1),C1与x轴的正半轴交与点A1 , 且其对称轴分别交抛物线C,C1于点B1 , D1 , 此时四边形OB1A1D1恰为正方形;按上述类似方法,如图2,抛物线C1:y1=a1x(x﹣b1)经过变换可得到抛物线C2:y2=a2x(x﹣b2),C2与x轴的正半轴交与点A2 , 且其对称轴分别交抛物线C1 , C2于点B2 , D2 , 此时四边形OB2A2D2也恰为正方形;按上述类似方法,如图3,可得到抛物线C3:y3=a3x(x﹣b3)与正方形OB3A3D3 . 请探究以下问题: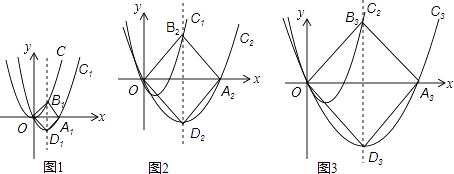
(1)填空:a1= , b1=;
(2)求出C2与C3的解析式;
(3)按上述类似方法,可得到抛物线Cn:yn=anx(x﹣bn)与正方形OBnAnDn(n≥1).
①请用含n的代数式直接表示出Cn的解析式;
②当x取任意不为0的实数时,试比较y2015与y2016的函数值的大小并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:
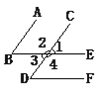
(1)如果∠1=∠B,那么_______∥_______,根据是__________________________;
(2)如果∠3=∠D,那么_______∥_______,根据是__________________________;
(3)如果要使BE∥DF,必须∠1=∠_______,根据是_________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OA⊥OB,∠AOD=∠BOC由此判定OC⊥OD,下面是推理过程,请填空.

解:∵OA⊥OB(已知)
所以_____=90°(________)
因为_____=∠AOD-∠AOC,____=∠BOC-∠AOC,∠AOD=∠BOC,
所以______=_____(等量代换)
所以______=90°
所以OC⊥OD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com