
����Ŀ����ͼ1��������C��y=x2�����仯�ɵõ�������C1��y1=a1x��x��b1����C1��x��������ύ���A1 �� ����Գ���ֱ�������C��C1�ڵ�B1 �� D1 �� ��ʱ�ı���OB1A1D1ǡΪ�����Σ����������Ʒ�������ͼ2��������C1��y1=a1x��x��b1�������任�ɵõ�������C2��y2=a2x��x��b2����C2��x��������ύ���A2 �� ����Գ���ֱ�������C1 �� C2�ڵ�B2 �� D2 �� ��ʱ�ı���OB2A2D2ҲǡΪ�����Σ����������Ʒ�������ͼ3���ɵõ�������C3��y3=a3x��x��b3����������OB3A3D3 �� ��̽���������⣺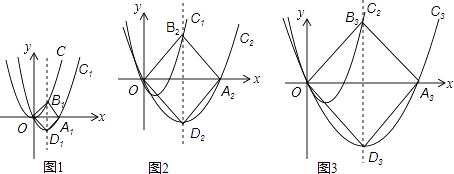
��1����գ�a1= �� b1=��
��2�����C2��C3�Ľ���ʽ��
��3�����������Ʒ������ɵõ�������Cn��yn=anx��x��bn����������OBnAnDn��n��1����
�����ú�n�Ĵ���ʽֱ�ӱ�ʾ��Cn�Ľ���ʽ��
�ڵ�xȡ���ⲻΪ0��ʵ��ʱ���ԱȽ�y2015��y2016�ĺ���ֵ�Ĵ�С��˵�����ɣ�
���𰸡�
��1��1��2
��2��
�⣺y2=0ʱ��a2x��x��b2��=0��
x1=0��x2=b2��
��A2��b2��0����
��������OB2A2D2�ã�OA2=B2D2=b2��
��B2�� ![]() ��
�� ![]() ����
����
��B2��������c1�ϣ��� ![]() =��
=�� ![]() ��2��2��
��2��2�� ![]() ��
��
b2��b2��6��=0��
b2=0�����������⣩��b2=6��
��D2��3����3����
��D2��3����3������C2�Ľ���ʽ����3=3a2��3��6����a2= ![]() ��
��
��C2�Ľ���ʽ��y2= ![]() x��x��6��=
x��x��6��= ![]() x2��2x��
x2��2x��
y3=0ʱ��a3x��x��b3��=0��
x1=0��x2=b3��
��A3��b3��0����
��������OB3A3D3�ã�OA3=B3D3=b3��
��B3�� ![]() ��
�� ![]() ����
����
��B3��������C2�ϣ��� ![]() =
= ![]() ��
�� ![]() ��2��2��
��2��2�� ![]() ��
��
b3��b3��18��=0��
b3=0�����������⣩��b3=18��
��D3��9����9����
��D3��9����9������C3�Ľ���ʽ����9=9a3��9��18����a3= ![]() ��
��
��C3�Ľ���ʽ��y3= ![]() x��x��18��=
x��x��18��= ![]() ��2x��
��2x��
��3��
�⣺��Cn�Ľ���ʽ��yn= ![]() x2��2x��n��1����
x2��2x��n��1����
��������ɵ�������C2015�Ľ���ʽΪ��y2015= ![]() x2��2x��
x2��2x��
������C2016�Ľ���ʽΪ��y2016= ![]() x2��2x��
x2��2x��
���������ߵĽ���Ϊ��0��0����
�൱x��0ʱ��y2015��y2016����x��0ʱ��y2015��y2016��
���������⣺��1��y1=0ʱ��a1x��x��b1��=0��
x1=0��x2=b1 ��
��A1��b1 �� 0����
��������OB1A1D1�ã�OA1=B1D1=b1 ��
��B1�� ![]() ��
�� ![]() ����D1��
����D1�� ![]() ����
���� ![]() ����
����
��B1��������c�ϣ��� ![]() =
= ![]() ��
��
b1��b1��2��=0��
b1=0�����������⣩��b1=2��
��D1��1����1����
��D1��1����1������y1=a1x��x��b1���еã���1=��a1 ��
��a1=1��
�ʴ�Ϊ��1��2��
��1������x�ύ��A1���꣬���������ζԽ������ʱ�ʾ��B1�����꣬�����Ӧ�Ľ���ʽ���������Ӧ��b1��ֵ��д��D1�����꣬����y1�Ľ���ʽ�п����a1��ֵ����2������x�ύ��A2���꣬���������ζԽ������ʱ�ʾ��B2�����꣬�����Ӧ�Ľ���ʽ���������Ӧ��b2��ֵ��д��D2�����꣬����y2�Ľ���ʽ�п����a2��ֵ��д��������C2�Ľ���ʽ����������ͬ�ķ�����������C3�Ľ���ʽ����3���ٸ���ͼ�α任�������ϵ������ó�an=a1=1����B1���꣨1��1����B2���꣨3��3����B3���꣨7��7����Bn���꣨2n��1��2n��1������bn=2��2n��1��=2n+1��2��n��1����д��������Cn����ʽ��������������C2015��������C2016�Ľ���Ϊ��0��0�����ڽ��������۲�ͼ�εó�y2015��y2016�ĺ���ֵ�Ĵ�С��


 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������C�ǡ�O��һ�㣬AD����C�������ഹֱ������ΪD��ֱ��DC��AB���ӳ����ཻ��P����CEƽ�֡�ACB����ֱ��AB�ڵ�F������BE�� 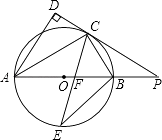
��1����֤��ACƽ�֡�DAB��
��2��̽���߶�PC��PF֮��Ĵ�С��ϵ��������֤����
��3����tan��PCB= ![]() ��BE=
��BE= ![]() ����PF�ij���
����PF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������С���������Ӧ�Ľ��:
(1)��ͬλ����ȣ���ֱ��ƽ����������ֱ��ƽ�У�ͬλ������������������������ͽ����������е�λ��ǡ�öԵ����ǰ�����һ���������һ������������⣬����д����������ƽ�����ϵĵ㵽�����ߵľ���������������⣬��ָ�������������ͽ��ۣ�
(2)���������������ͼ�Σ���д�����������������.
��֪����ֱ��AB��һ��O��������OC��OM��ON�ֱ�ƽ����AOC����BOC����OM��ON.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�BC=a��AC=b��AB=c��b��c��a����BC�Ĵ�ֱƽ����DG����BAC�Ľ�ƽ����AD�ڵ�D��DE��AB��E��DF��AC��F�������н���һ���������ǣ�������
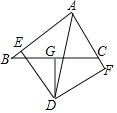
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��3.3����2��0��![]() ����3.5.
����3.5.
(1) �Ƚ���Щ���Ĵ�С������������������������
(2) �Ƚ���Щ���ľ���ֵ�Ĵ�С��������Щ���ľ���ֵ��������������������
(3) �Ƚ���Щ�����෴���Ĵ�С��������Щ�����෴����������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ,����ABC����ijһ����ƽ��һ���ľ���õ���MNL,�����н�������ȷ�������� ��
��AM��BN����AM=BN����BC=ML���ܡ�ACB=��MNL��
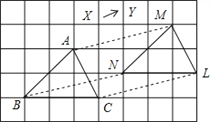
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AB��BC��AC���ߵij��ֱ�Ϊ![]() ��
�� ![]() ��
�� ![]() ������������ε������С��ͬѧ�ڽ�������ʱ���Ȼ�һ������������ÿ��С�����εı߳�Ϊ1�������������л��������ABC������ABC�������㶼��С�����εĶ��㴦������ͼ1��ʾ��������������ABC�ĸߣ�������������ܼ�������������
������������ε������С��ͬѧ�ڽ�������ʱ���Ȼ�һ������������ÿ��С�����εı߳�Ϊ1�������������л��������ABC������ABC�������㶼��С�����εĶ��㴦������ͼ1��ʾ��������������ABC�ĸߣ�������������ܼ�������������
��1����ABC�������������������
��2������DEF������DE��EF��DF���ֱ�Ϊ![]() ��
�� ![]() ��
�� ![]() ������ͼ2�������������л�����Ӧ����DEF���������DEF�����Ϊ��������������
������ͼ2�������������л�����Ӧ����DEF���������DEF�����Ϊ��������������
��3������ABC�У�AB=2![]() ��AC=4��BC=2����ABΪ������ABC������ABD��D��C��AB��ࣩ��ʹ��ABDΪ����ֱ�������Σ����߶�CD�ij�Ϊ��������������
��AC=4��BC=2����ABΪ������ABC������ABD��D��C��AB��ࣩ��ʹ��ABDΪ����ֱ�������Σ����߶�CD�ij�Ϊ��������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ֽƬOABC����ƽ��ֱ������ϵ�У�OΪԭ�㣬��A��x���ϣ���C��y���ϣ�OA=10��OC=8����ͼ��OC����ȡһ��D������BCD��BD�۵���ʹ��Cǡ������OA���ϣ�����E�㣻
��1�����E�����꼰�ۺ�DB�ij���
��2����x����ȡ����M��N����M�ڵ�N����ࣩ����MN=4.5����ʹ�ı���BDMN���ܳ���̵ĵ�M����N�����ꡣ
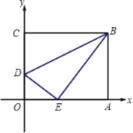
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���ABCD�У�E��CD�ϵ�һ������AE��BE����ͼ�����ĸ���������AEƽ����BAD����BEƽ����ABC����AE��EB����AB=AD+BC������������������Ϊ�����������д��һ�����Ƴ�AD��BC����ȷ���⣬������֤����
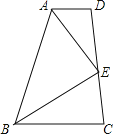
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com