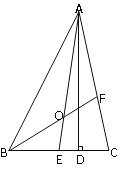
[题目]如图.△ABC中.AD是高.AE.BF是角平分线.它们相交于点O.∠BAC=50°.∠C=70°.求∠DAC及∠BOA的度数. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠BAC=50°，∠C=70°，求∠DAC及∠BOA的度数.

【答案】∠DAC=20°，∠BOA=125°．

【解析】试题分析：根据AD⊥BC，则∠ADC=90°，根据△ADC的内角和可以求出∠DAC的度数，根据△ABC的内角和求出∠ABC的度数，然后根据角平分线的性质求出∠ABO+∠BAO的度数，最后根据△ABO的内角和求出∠BOA的度数．

试题解析：∵AD是高 ∴∠ADC=90° ∵∠C=70°∴∠DAC=180°﹣90°﹣70°=20°

∵∠BAC=50°，∠C=70°，AE是角平分线 ∴∠BAO=25°，∠ABC=60°

∵BF是∠ABC的角平分线 ∴∠ABO=30° ∴∠BOA=180°﹣∠BAO﹣∠ABO=125°

练习册系列答案

成长记寒假总动员云南科技出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

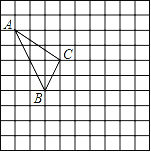
【题目】在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A、C的坐标分别为（﹣4，5），（﹣1，3）．

（1）请在如图所示的网格平面内作出平面直角坐标系；

（2）请作出△ABC关于y轴对称的△A′B′C′；

（3）点B′的坐标为　　．

（4）△ABC的面积为　　．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△OAB中，OA=OB，C为AB中点，以O圆心，OC长为半径作圆，AO与⊙O交于点E，直线OB与⊙O交于点F和D，连接EF、CF，CF与OA交于点G.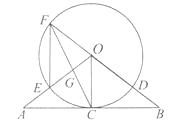

（1）求证：直线AB是⊙O的切线；
（2）求证：OD·EG=OG·EF；
（3）若AB=8，BD=2，求⊙O的半径.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】△ABC在平面直角坐标系中的位置如图所示.

（1）作出△ABC关于轴对称的△A1B1C1，并写出△A1B1C1各顶点的坐标；

（2）将△ABC向右平移6个单位，作出平移后的△A2B2C2，并写出△A2B2C2各顶点的坐标；

（3）观察△A1B1C和△A2B2C2，它们是否关于某直线对称？若是，请用实线条画出对称轴。

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】为增强市民的节能意识，我市试行阶梯电价.从2013年开始，按照每户每年的分三个档次计费，具体规定见下图.小明统计了自己2013年前5个月的实际用电量为1300度，请帮助小明分析下面问题.

（1）若小明家计划2013年全年的用电量不超过2520度，则6至12月份小明家平均每月用电量最多为多少度？（保留整数）

（2）若小明家2013年6月至12月份平均每月用电量等于前5个月的平均每月用电量，则小明家2013年应交总电费多少元？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，AB =AC=2，∠B = 40°，点D在线段BC上运动（不与点B，C重合），连接AD，作∠ADE = 40°，DE交线段AC于点E．

（1）当∠BDA = 115°时，∠BAD= °，∠DEC = °，当点D从点B向点C运动时，∠BDA逐渐变（填“大”或“小”）．

（2）当DC等于多少时，△ABD≌△DCE？请说明理由．

（3）在点D的运动过程中，是否存在△ADE是等腰三角形？若存在，请直接写出此时∠BDA的度数；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图1，在平面直角坐标系xOy中，点A（，0），B（3 ，0），以AB为直径的⊙G交y轴于C，D两点.

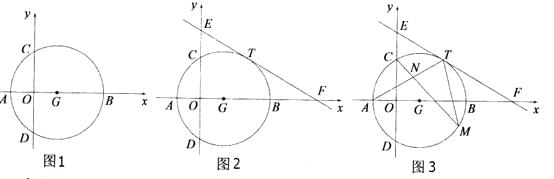
（1）填空：请直接写出⊙G的半径r，圆心G的坐标：r=；G（，）.
（2）如图2，直线y= 与x、y轴分别交于F、E两点，且经过圆上一点T（，m），求证：直线EF是⊙G的切线；
（3）在（2）的条件下，如图3，点M是⊙G优弧上的一个动点（不包括A、T两点），连接AT、CM、TM，CM交AT于点N，试问，是否存在一个常数k，始终满足CN·CM=k？如果存在，请求出k的值，如果不存在，请说明理由.