
【题目】如图,在△OAB中,OA=OB,C为AB中点,以O圆心,OC长为半径作圆,AO与⊙O交于点E,直线OB与⊙O交于点F和D,连接EF、CF,CF与OA交于点G.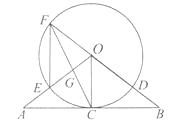
(1)求证:直线AB是⊙O的切线;
(2)求证:OD·EG=OG·EF;
(3)若AB=8,BD=2,求⊙O的半径.
【答案】
(1)
解:证明:∵OA=OB,C为AB中点,
∴OC⊥AB,
∴直线AB是⊙O的切线.
(2)
解:证明:∵OA=OB,C为AB中点,
∴∠AOC=∠BOC,
∴ ![]() ,
,
∴∠EFC=∠DFC,
∵OF=OC,
∴∠OFC=∠OCF,
∴∠EFC=∠OCF,
又∵∠EGF=∠OGC,
∴△EGF∽△OGC,
∴ ![]() ,
,
∵OD=OC,
∴ ![]() ,
,
∴ OD·EG=OG ·EF.
(3)
解:∵AB=8,C为AB中点,
∴BC=4,
设⊙O的半径为r,
∵在Rt△OCB中,OC2+BC2=OB2,
∴r2+42=(r+2)2,
解得:r=3,
∴⊙O 的半径为3.
【解析】(1)由等腰三角形的“三线合一”易得OC⊥AB,即直线AB是⊙O的切线;(2)要证OD·EG=OG·EF,就要证 ![]() ,而OD=OC,就要证
,而OD=OC,就要证 ![]() ,则要证△EGF∽△OGC,而∠EGF=∠OGC,只需要证∠EFC=∠OCF即可;(3)在Rt△OCB中,⊙O的半径为r,由勾股定理构造方程解答.
,则要证△EGF∽△OGC,而∠EGF=∠OGC,只需要证∠EFC=∠OCF即可;(3)在Rt△OCB中,⊙O的半径为r,由勾股定理构造方程解答.


科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30o,点A1、A2、A3 在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7 的边长为【 】

A.6 B.12 C.32 D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() (x+2)(x﹣4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(x+2)(x﹣4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.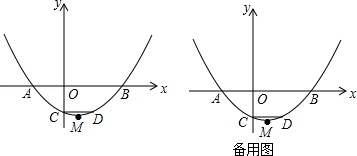
(1)求点A、B、C的坐标;
(2)设动点N(﹣2,n),求使MN+BN的值最小时n的值;
(3)P是抛物线上一点,请你探究:是否存在点P,使以P、A、B为顶点的三角形与△ABD相似(△PAB与△ABD不重合)?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳市民中心广场上有旗杆如图①所示,某学校数学兴趣小组测量了该旗杆的高度.如图②,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为16米,落在斜坡上的影长CD为8米,AB⊥BC;同一时刻,太阳光线与水平面的夹角为 45°,1米的标杆EF竖立在斜坡上的影长FG为2米,求旗杆的高度.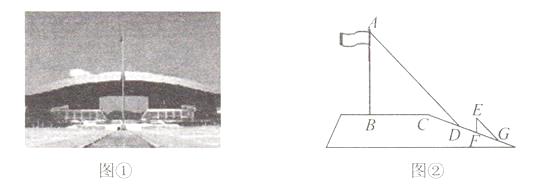
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①是一个重要公式的几何解释.请你写出这个公式;
(2)如图②,Rt△ABC≌Rt△CDE,∠B=∠D=90°,且B、C、D三点在一条直线上.试证明∠ACE=90°;
(3)伽菲尔德(G a rfield,1881年任美国第20届总统)利用(1)中的公式和图②证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),现请你尝试该证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
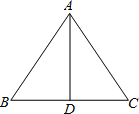
【题目】如图,AD是△ABC的边BC上的中线,由下列条件中的某一个就能推出△ABC是等腰三角形的是______(把所有的正确答案的序号都填在横线上)①∠BAD=∠ACD;②∠BAD+∠B=∠CAD+∠C;③AB+BD=AC+CD;④AB-BD=AC-CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形 ![]() 的对角线
的对角线 ![]() ,
, ![]() 相交于点
相交于点 ![]() .
.
(1)如图1, ![]() ,
, ![]() 分别是
分别是 ![]() ,
, ![]() 上的点,
上的点, ![]() 与
与 ![]() 的延长线相交于点
的延长线相交于点 ![]() .若
.若 ![]() ,求证:
,求证: ![]() ;
;
(2)如图2, ![]() 是
是 ![]() 上的点,过点
上的点,过点 ![]() 作
作 ![]() ,交线段
,交线段 ![]() 于点
于点 ![]() ,连结
,连结 ![]() 交
交 ![]() 于点
于点 ![]() ,交
,交 ![]() 于点
于点 ![]() .若
.若 ![]() ,
,
①求证: ![]() ;
;
②当 ![]() 时,求
时,求 ![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com