
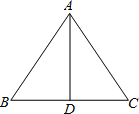
【题目】如图,AD是△ABC的边BC上的中线,由下列条件中的某一个就能推出△ABC是等腰三角形的是______(把所有的正确答案的序号都填在横线上)①∠BAD=∠ACD;②∠BAD+∠B=∠CAD+∠C;③AB+BD=AC+CD;④AB-BD=AC-CD
【答案】②③④
【解析】
可根据等腰三角形三线合一的性质来判断①②是否正确; ③④要通过作等腰三角形来判断其结论是否成立
解: ②当∠BAD=∠CAD时,![]() AD是∠BAC的平分线, 且AD是BC边上的
AD是∠BAC的平分线, 且AD是BC边上的
高;则ΔABD≌ΔACD,![]() ΔBAC是等腰三角形;
ΔBAC是等腰三角形;
③延长DB至E,使BE=AB;延长DC至F,
使CF=AC; 连接AE, AF;
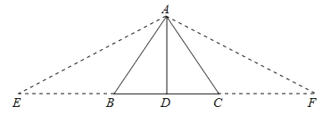
![]() AB+BD=CD+AC,
AB+BD=CD+AC,
![]() DE=DF,又AD⊥BC;
DE=DF,又AD⊥BC;
![]() ΔAEF是等腰三角形;
ΔAEF是等腰三角形;![]() ∠E=∠F;
∠E=∠F;
![]() AB=BE,
AB=BE, ![]() ∠ABC=2∠E,同理可得,∠ACB=2∠F,
∠ABC=2∠E,同理可得,∠ACB=2∠F,
![]() ∠ABC=∠ACB,即:AB=AC,
∠ABC=∠ACB,即:AB=AC,
![]() ΔABC是等腰三角形;
ΔABC是等腰三角形;
④在ΔABC中, AD⊥BC, 根据勾股定理, 得:
AB![]() -BD
-BD![]() =AC-
=AC-![]() CD
CD![]() .即
.即
(AB+BD)(AB-BD)=(AC+CD)(AC-CD)
![]() AB-BD=AC-CD①,
AB-BD=AC-CD①,
![]() AB+BD=AC+CD②;
AB+BD=AC+CD②;
+②得:2AB=2AC;
![]() AB=AC,
AB=AC,
![]() ΔABC是等腰三角形
ΔABC是等腰三角形
故答案为:②③④.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )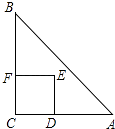
A.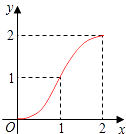
B.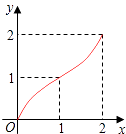
C.
D.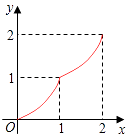
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】潮州旅游文化节开幕前,某凤凰茶叶公司预测今年凤凰茶叶能够畅销,就用32000元购进了一批凤凰茶叶,上市后很快脱销,茶叶公司又用68000元购进第二批凤凰茶叶,所购数量是第一批购进数量的2倍,但每千克凤凰茶叶进价多了10元.
(1)该凤凰茶叶公司两次共购进这种凤凰茶叶多少千克?
(2)如果这两批茶叶每千克的售价相同,且全部售完后总利润率不低于20%,那么每千克售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△OAB中,OA=OB,C为AB中点,以O圆心,OC长为半径作圆,AO与⊙O交于点E,直线OB与⊙O交于点F和D,连接EF、CF,CF与OA交于点G.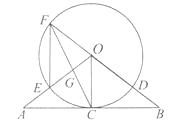
(1)求证:直线AB是⊙O的切线;
(2)求证:OD·EG=OG·EF;
(3)若AB=8,BD=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点A(0,6)的直线AB与直线OC相交于点C(2,4)动点P沿路线O→C→B运动.(1)求直线AB的解析式;(2)当△OPB的面积是△OBC的面积的![]() 时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.
时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于![]() 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强市民的节能意识,我市试行阶梯电价.从2013年开始,按照每户每年的分三个档次计费,具体规定见下图.小明统计了自己2013年前5个月的实际用电量为1300度,请帮助小明分析下面问题.

(1)若小明家计划2013年全年的用电量不超过2520度,则6至12月份小明家平均每月用电量最多为多少度?(保留整数)
(2)若小明家2013年6月至12月份平均每月用电量等于前5个月的平均每月用电量,则小明家2013年应交总电费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,点A( ![]() ,0),B(3
,0),B(3 ![]() ,0),以AB为直径的⊙G交y轴于C,D两点.
,0),以AB为直径的⊙G交y轴于C,D两点.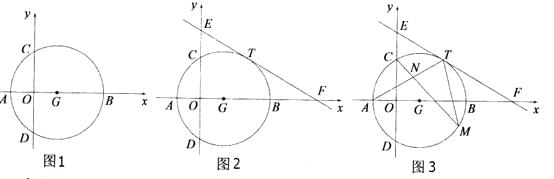
(1)填空:请直接写出⊙G的半径r,圆心G的坐标:r=;G( , ).
(2)如图2,直线y= ![]() 与x、y轴分别交于F、E两点,且经过圆上一点T(
与x、y轴分别交于F、E两点,且经过圆上一点T( ![]() ,m),求证:直线EF是⊙G的切线;
,m),求证:直线EF是⊙G的切线;
(3)在(2)的条件下,如图3,点M是⊙G优弧 ![]() 上的一个动点(不包括A、T两点),连接AT、CM、TM,CM交AT于点N,试问,是否存在一个常数k,始终满足CN·CM=k?如果存在,请求出k的值,如果不存在,请说明理由.
上的一个动点(不包括A、T两点),连接AT、CM、TM,CM交AT于点N,试问,是否存在一个常数k,始终满足CN·CM=k?如果存在,请求出k的值,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
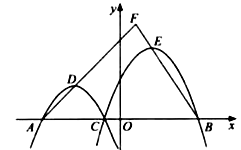
【题目】如图,在平面直角坐标系 ![]() 中,已知
中,已知 ![]() ,
, ![]() 两点的坐标分别为
两点的坐标分别为 ![]() ,
, ![]() ,
, ![]() 是线段
是线段 ![]() 上一点(与
上一点(与 ![]() ,
, ![]() 点不重合),抛物线
点不重合),抛物线 ![]()
![]() (
( ![]() )经过点
)经过点 ![]() ,
, ![]() ,顶点为
,顶点为 ![]() ,抛物线
,抛物线 ![]()
![]() (
( ![]() )经过点
)经过点 ![]() ,
, ![]() ,顶点为
,顶点为 ![]() ,
, ![]() ,
, ![]() 的延长线相交于点
的延长线相交于点 ![]() .
.
(1)若 ![]() ,
, ![]() ,求抛物线
,求抛物线 ![]() ,
, ![]() 的解析式;
的解析式;
(2)若 ![]() ,
, ![]() ,求
,求 ![]() 的值;
的值;
(3)是否存在这样的实数 ![]() (
( ![]() ),无论
),无论 ![]() 取何值,直线
取何值,直线 ![]() 与
与 ![]() 都不可能互相垂直?若存在,请直接写出
都不可能互相垂直?若存在,请直接写出 ![]() 的两个不同的值;若不存在,请说明理由.
的两个不同的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com