
【题目】如图,已知抛物线y= ![]() (x+2)(x﹣4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(x+2)(x﹣4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.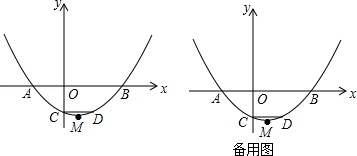
(1)求点A、B、C的坐标;
(2)设动点N(﹣2,n),求使MN+BN的值最小时n的值;
(3)P是抛物线上一点,请你探究:是否存在点P,使以P、A、B为顶点的三角形与△ABD相似(△PAB与△ABD不重合)?若存在,求出点P的坐标;若不存在,说明理由.
【答案】
(1)
解:令y=0得x1=﹣2,x2=4,
∴点A(﹣2,0)、B(4,0)
令x=0得y=﹣ ![]() ,
,
∴点C(0,﹣ ![]() )
)
(2)
解:将x=1代入抛物线的解析式得y=﹣ ![]()
∴点M的坐标为(1,﹣ ![]() )
)
∴点M关于直线x=﹣2的对称点M′的坐标为(﹣5, ![]() )
)
设直线M′B的解析式为y=kx+b
将点M′、B的坐标代入得: 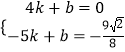
解得: 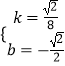
所以直线M′B的解析式为y= ![]() .
.
将x=﹣2代入得:y=﹣ ![]() ,
,
所以n=﹣ ![]()
(3)
解:过点D作DE⊥BA,垂足为E.
由勾股定理得:
AD= ![]() =3
=3 ![]() ,
,
BD= ![]() ,
,
如下图,①当P1AB∽△ADB时,
![]() 即:
即: ![]()
∴P1B=6 ![]()
过点P1作P1M1⊥AB,垂足为M1.
∴ ![]() 即:
即: ![]()
解得:P1M1=6 ![]() ,
,
∵ ![]() 即:
即: ![]()
解得:BM1=12
∴点P1的坐标为(﹣8,6 ![]() )
)
∵点P1不在抛物线上,所以此种情况不存在;
②当△P2AB∽△BDA时, ![]() 即:
即: ![]()
∴P2B=6 ![]()
过点P2作P2M2⊥AB,垂足为M2.
∴ ![]() ,即:
,即: ![]()
∴P2M2=2 ![]()
∵ ![]() ,即:
,即: ![]()
∴M2B=8
∴点P2的坐标为(﹣4,2 ![]() )
)
将x=﹣4代入抛物线的解析式得:y=2 ![]() ,
,
∴点P2在抛物线上.
由抛物线的对称性可知:点P2与点P4关于直线x=1对称,
∴P4的坐标为(6,2 ![]() ),
),
当点P3位于点C处时,两三角形全等,所以点P3的坐标为(0,﹣ ![]() ),
),
综上所述点P的坐标为:(﹣4,2 ![]() )或(6,2
)或(6,2 ![]() )或(0,﹣
)或(0,﹣ ![]() )时,以P、A、B为顶点的三角形与△ABD相似
)时,以P、A、B为顶点的三角形与△ABD相似
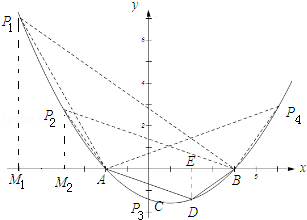
【解析】(1)令y=0可求得点A、点B的横坐标,令x=0可求得点C的纵坐标;(2)根据两点之间线段最短作M点关于直线x=﹣2的对称点M′,当N(﹣2,N)在直线M′B上时,MN+BN的值最小;(3)需要分类讨论:△PAB∽△ABD、△PAB∽△ABD,根据相似三角形的性质求得PB的长度,然后可求得点P的坐标.
【考点精析】通过灵活运用二次函数的图象和二次函数的性质,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.


科目:初中数学 来源: 题型:
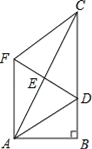
【题目】如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
求证:四边形ADCF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )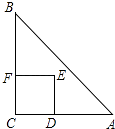
A.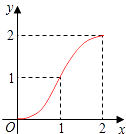
B.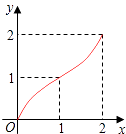
C.
D.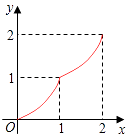
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)点B′的坐标为 .
(4)△ABC的面积为 .
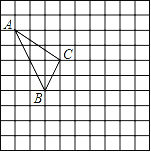
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF= ![]() ∠CAB.
∠CAB. 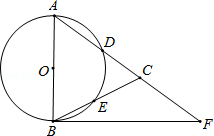
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF= ![]() ,求BC和BF的长.
,求BC和BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D为边BC的中点,过点A作射线AE,过点C作CF⊥AE于点F,过点B作BG⊥AE于点G,连接FD并延长,交BG于点H.
(1)求证:DF=DH;
(2)若∠CFD=120°,求证:△DHG为等边三角形.
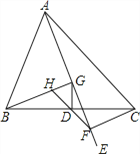
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】潮州旅游文化节开幕前,某凤凰茶叶公司预测今年凤凰茶叶能够畅销,就用32000元购进了一批凤凰茶叶,上市后很快脱销,茶叶公司又用68000元购进第二批凤凰茶叶,所购数量是第一批购进数量的2倍,但每千克凤凰茶叶进价多了10元.
(1)该凤凰茶叶公司两次共购进这种凤凰茶叶多少千克?
(2)如果这两批茶叶每千克的售价相同,且全部售完后总利润率不低于20%,那么每千克售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△OAB中,OA=OB,C为AB中点,以O圆心,OC长为半径作圆,AO与⊙O交于点E,直线OB与⊙O交于点F和D,连接EF、CF,CF与OA交于点G.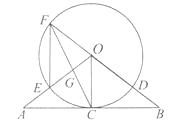
(1)求证:直线AB是⊙O的切线;
(2)求证:OD·EG=OG·EF;
(3)若AB=8,BD=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,点A( ![]() ,0),B(3
,0),B(3 ![]() ,0),以AB为直径的⊙G交y轴于C,D两点.
,0),以AB为直径的⊙G交y轴于C,D两点.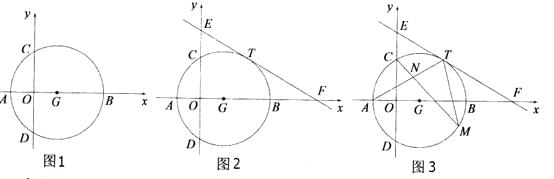
(1)填空:请直接写出⊙G的半径r,圆心G的坐标:r=;G( , ).
(2)如图2,直线y= ![]() 与x、y轴分别交于F、E两点,且经过圆上一点T(
与x、y轴分别交于F、E两点,且经过圆上一点T( ![]() ,m),求证:直线EF是⊙G的切线;
,m),求证:直线EF是⊙G的切线;
(3)在(2)的条件下,如图3,点M是⊙G优弧 ![]() 上的一个动点(不包括A、T两点),连接AT、CM、TM,CM交AT于点N,试问,是否存在一个常数k,始终满足CN·CM=k?如果存在,请求出k的值,如果不存在,请说明理由.
上的一个动点(不包括A、T两点),连接AT、CM、TM,CM交AT于点N,试问,是否存在一个常数k,始终满足CN·CM=k?如果存在,请求出k的值,如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com