
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中正确的有( )
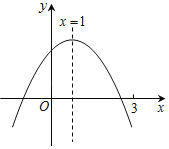
A.①②③B.②④C.②⑤D.②③⑤
【答案】C
【解析】
由抛物线的开口方向、抛物线的对称轴及抛物线与![]() 轴的交点判断①②,由顶点坐标确定函数最大值是a+b+c判断③,然后根据抛物线与
轴的交点判断①②,由顶点坐标确定函数最大值是a+b+c判断③,然后根据抛物线与![]() 轴交点的个数及对称轴判断④,由ax12+bx1=ax22+bx2恒等变形得x1+x2=
轴交点的个数及对称轴判断④,由ax12+bx1=ax22+bx2恒等变形得x1+x2=![]() ,根据对称轴直线x=
,根据对称轴直线x=![]() =1,可以判断⑤.
=1,可以判断⑤.
∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为直线x=![]() =1,
=1,
∴b=﹣2a>0,即2a+b=0,所以②正确;
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①错误;
∵抛物线对称轴为直线x=1,
∴函数的最大值为a+b+c,
∴当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm,所以③错误;
∵抛物线与x轴的一个交点在(3,0)的左侧,而对称轴为直线x=1,
∴抛物线与x轴的另一个交点在(﹣1,0)的右侧
∴当x=﹣1时,y<0,
∴a﹣b+c<0,所以④错误;
∵ax12+bx1=ax22+bx2,
∴ax12+bx1﹣ax22﹣bx2=0,
∴a(x1+x2)(x1﹣x2)+b(x1﹣x2)=0,
∴(x1﹣x2)[a(x1+x2)+b]=0,
而x1≠x2,
∴a(x1+x2)+b=0,即x1+x2=![]() ,
,
∵b=﹣2a,
∴x1+x2=2,所以⑤正确.
综上所述,正确的有②⑤.
故选:C.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有两个实数根x1,x2.
有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)是否存在实数k使得![]() 成立?若存在,请求出k的值;若不存在,请说明理由.
成立?若存在,请求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )

A. 21.7米 B. 22.4米 C. 27.4米 D. 28.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年国庆期间解放碑、洪崖洞、朝天门、来福士、长嘉汇等景点人员密集;穿楼而过的轻轨、洪崖洞、灯光秀……吸引着海量游客前来重庆打卡.位于洪崖洞的重庆知名火锅小天鹅火锅在节日期间每天也人满为患,其中鸳鸯火锅和红汤火锅最受游客青睐.在中秋节期间,前来就餐选择鸳鸯火锅和红汤火锅的游客共有2000名,鸳鸯火锅和红汤火锅的人均消费分别为180元和120元.
(1)中秋节期间,若选择红汤火锅的人数不超过鸳鸯火锅人数的1.5倍.求至少有多少人选择鸳鸯火锅?
(2)“国庆”节期间,前来就餐的游客人数有所下降,与(1)问中选择鸳鸯火锅的人数最少时相比,选择两种火锅的人数均下降了a%;人均消费与中秋节期间相比均有所上升,其中鸳鸯火锅的人均消费上涨了a%,红汤火锅的人均消费上涨了![]() a%,最终“国庆”节期间两种火锅的总销售额与(1)问中选择鸳鸯火锅的人数最少时的两种火锅的总销售额持平,求a的值.
a%,最终“国庆”节期间两种火锅的总销售额与(1)问中选择鸳鸯火锅的人数最少时的两种火锅的总销售额持平,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
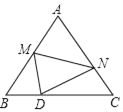
【题目】如图,等边△ABC的边长为10,点M是边AB上一动点,将等边△ABC沿过点M的直线折叠,该直线与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,折痕为MN,则AN的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D为直线BC上一动点(点D不与B、C重合)以AD为边作正方形ADEF,使∠DAF=∠BAC,连接CF.
(1)如图1,当点D在线段BC上时,求证:BD=CF;
(2)如图2,当点D在线段BC的延长线上,且∠BAC=90°时.
①问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
②延长BA交CF于点G,连接GE,若AB=2![]() ,CD=BC,请求出GE的长.
,CD=BC,请求出GE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.设每个房间定价增加10x元(x为整数).
(1)直接写出每天游客居住的房间数量y与x的函数关系式;
(2)设宾馆每天的利润为w元,当每间房价定价为多少元时,宾馆每天所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 与一次函数y=x+b的图形在第一象限相交于点A(1,﹣k+4).
与一次函数y=x+b的图形在第一象限相交于点A(1,﹣k+4).
(1)试确定这两函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并求△AOB的面积;
(3)根据图象直接写出反比例函数值大于一次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李的活鱼批发店以 44 元/公斤的价格从港口买进一批 2000 公斤的某品种活鱼,在运输过程中,有部分鱼未能存活,小李对运到的鱼进行随机抽查,结果如表一.由于 市场调节,该品种活鱼的售价与日销售量之间有一定的变化规律,表二是近一段时间该批发店的销售记录.
表一
所抽查的鱼的总重量 m(公斤) | 100 | 150 | 200 | 250 | 350 | 450 | 500 |
存活的鱼的重量与 m 的比值 | 0.885 | 0.876 | 0.874 | 0.878 | 0.871 | 0.880 | 0.880 |
表二
该品种活鱼的售价(元/公斤) | 50 | 51 | 52 | 53 | 54 |
该品神活鱼的日销售量(公斤) | 400 | 360 | 320 | 280 | 240 |
(1)请估计运到的 2000 公斤鱼中活鱼的总重量;(直接写出答案)
(2)按此市场调节的观律,
①若该品种活鱼的售价定为 52.5 元/公斤,请估计日销售量,并说明理由;
②考虑到该批发店的储存条,小李打算 8 天内卖完这批鱼(只卖活鱼),且售价保持 不变,求该批发店每日卖鱼可能达到的最大利润,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com