
 С���ͰְִӼҲ���ȥ�����ְ��ȳ���һֱ����ǰ�У�С����������ҵ����ľ���Ϊ2500m����ͼ��С���Ͱְ�����·��s��m���벽��ʱ��t��min���ĺ���ͼ��
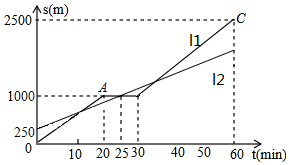
С���ͰְִӼҲ���ȥ�����ְ��ȳ���һֱ����ǰ�У�С����������ҵ����ľ���Ϊ2500m����ͼ��С���Ͱְ�����·��s��m���벽��ʱ��t��min���ĺ���ͼ������ ��1����ͼ���֪��ֱ��l2��ʾ����С���İְ�����·���벽��ʱ��ĺ�����ϵʽ����
��2�����ô���ϵ�������ɽ�����⣮
��3�����÷��������������������ʱ�伴�ɣ�
��4���ֱ�����С���İְֵ��﹫��Ҫ��ʱ�䡢С�����﹫��Ҫ��ʱ�䣬���㼴�ɣ�
��� �⣺��1����ͼ���֪��ֱ��l2��ʾ����С���İְ�����·���벽��ʱ��ĺ�����ϵʽ��
�ʴ�Ϊl2��
��2����ֱ��l2������ϵʽΪ��s=kt+b���� $\left\{\begin{array}{l}{25k+b=1000}\\{b=250}\end{array}\right.$��
��� $\left\{\begin{array}{l}{k=30}\\{b=250}\end{array}\right.$��
��С���Ͱְ����ߵ�·���벽��ʱ��Ĺ�ϵʽΪ��s=30t+250��
��ֱ��BC�Ľ���ʽΪs=mt+n������$\left\{\begin{array}{l}{30m+n=1000}\\{60m+n=2500}\end{array}\right.$��
���$\left\{\begin{array}{l}{m=50}\\{n=-500}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪs=50t-500��
��3����$\left\{\begin{array}{l}{s=50t-500}\\{s=30t+250}\end{array}\right.$�����t=37.5min��
��С������37.5min��ְֵ����һ��������
��4��30t+250=2500��
��ã�t=75��
��С���İְֵ��﹫��Ҫ75min��
��С�����﹫��Ҫ��ʱ����60min��
��С��ϣ���Ȱְ���20min���﹫����С���ڲ��й�����ͣ����ʱ�������5min��
���� ���⿼�����һ�κ�����Ӧ�ã����մ���ϵ������һ�κ�������ʽ����������ͼ���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
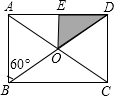 С������ͼ��ʾ�ľ���ֽ��ABCD����ǽ�ϣ�EΪAD�е㣬�ҡ�ABD=60�㣬�������������Ϸ��ÿ�η��ھ�����ֽ���ϣ���������Ӱ����ĸ�����$\frac{1}{8}$��
С������ͼ��ʾ�ľ���ֽ��ABCD����ǽ�ϣ�EΪAD�е㣬�ҡ�ABD=60�㣬�������������Ϸ��ÿ�η��ھ�����ֽ���ϣ���������Ӱ����ĸ�����$\frac{1}{8}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
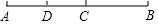 ��ͼ����C���߶�AB�ϣ���D��AC���е㣬���CB=$\frac{3}{2}$CD��AB=10.5cm����ôBC�ij�Ϊ��������
��ͼ����C���߶�AB�ϣ���D��AC���е㣬���CB=$\frac{3}{2}$CD��AB=10.5cm����ôBC�ij�Ϊ��������| A�� | A2.5cm | B�� | 3cm | C�� | 4.5cm | D�� | 6cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=4 | B�� | x=$\frac{9}{4}$ | C�� | x=-4 | D�� | x=$\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �Ķ�������ϣ�
�Ķ�������ϣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com