
 22、(1)如图,给出四个条件:①AE平分∠BAD,②BE平分∠ABC,③AE⊥EB,④AB=AD+BC.请你以其中三个作为命题的条件,写出一个能推出AD∥BC的正确命题,并加以证明;
22、(1)如图,给出四个条件:①AE平分∠BAD,②BE平分∠ABC,③AE⊥EB,④AB=AD+BC.请你以其中三个作为命题的条件,写出一个能推出AD∥BC的正确命题,并加以证明;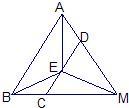
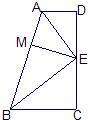 解:(1)如:①②④?AD∥BC.
解:(1)如:①②④?AD∥BC.

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
 23、如图,给出四个等式:①AE=AD;②AB=AC;③OB=OC:④∠B=∠C.现请你选取其中的三个,以某两个作为已知条件,另一个作为结论.
23、如图,给出四个等式:①AE=AD;②AB=AC;③OB=OC:④∠B=∠C.现请你选取其中的三个,以某两个作为已知条件,另一个作为结论.查看答案和解析>>
科目:初中数学 来源: 题型:
 21、如图,给出四个等式:①AE=AD;②AB=AC;③OB=OC;④∠B=∠C. 现选取其中的三个,以两个作为已知条件,另一个作为结论组成命题.
21、如图,给出四个等式:①AE=AD;②AB=AC;③OB=OC;④∠B=∠C. 现选取其中的三个,以两个作为已知条件,另一个作为结论组成命题.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,给出四个等式:①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.现选取其中的三个,以两个作为已知条件,另一个作为结论.
如图,给出四个等式:①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.现选取其中的三个,以两个作为已知条件,另一个作为结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com