
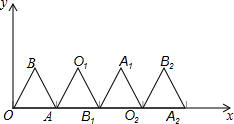
 如图,在平面直角坐标系中有一个等边△OBA,其中A点坐标为(1,0).将△OBA绕顶点A顺时针旋转120°,得到△AO1B1;将得到的△AO1B1绕顶点B1顺时针旋转120°,得到△B1A1O2;然后再将得到的△B1A1O2绕顶点O2顺时针旋转120°,得到△O2B2A2…按照此规律,继续旋转下去,则A2014点的坐标为
如图,在平面直角坐标系中有一个等边△OBA,其中A点坐标为(1,0).将△OBA绕顶点A顺时针旋转120°,得到△AO1B1;将得到的△AO1B1绕顶点B1顺时针旋转120°,得到△B1A1O2;然后再将得到的△B1A1O2绕顶点O2顺时针旋转120°,得到△O2B2A2…按照此规律,继续旋转下去,则A2014点的坐标为 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| 2 |
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
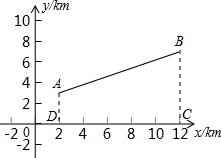 去冬今春,济宁市遭遇了200年不遇的大旱,某乡镇为了解决抗旱问题,要在某河道建一座水泵站,分别向河的同一侧张村A和李村B送水.经实地勘查后,工程人员设计图纸时,以河道上的大桥O为坐标原点,以河道所在的直线为x轴建立直角坐标系(如图).两村的坐标分别为A(2,3),B(12,7).
去冬今春,济宁市遭遇了200年不遇的大旱,某乡镇为了解决抗旱问题,要在某河道建一座水泵站,分别向河的同一侧张村A和李村B送水.经实地勘查后,工程人员设计图纸时,以河道上的大桥O为坐标原点,以河道所在的直线为x轴建立直角坐标系(如图).两村的坐标分别为A(2,3),B(12,7).查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 1×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5×7 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 100 |
| 201 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com