Question

15．已知：如图1，O为正方形ABCD的中心，分别延长OA到点F，OD到点E，使OF=2OA，OE=2OD，连结EF，将△FOE绕点O逆时针旋转α角得到△F′OE′（如图2）．
（1）证明AE′=BF′；
（2）当α=30°时，求证：△AOE′为直角三角形．

Answer 1

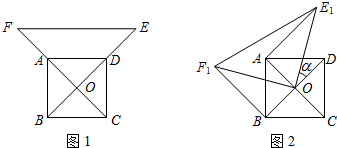
分析 （1）利用旋转不变量找到相等的角和线段，证得△E′AO≌△F′BO后即可证得结论；
（2）利用已知角，得出∠GAE′=∠GE′A=30°，从而证明直角三角形．

解答 （1）证明：∵O为正方形ABCD的中心，
∴OA=OD，
∵OF=2OA，OE=2OD，
∴OE=OF，
∵将△EOF绕点O逆时针旋转α角得到△E′OF′，
∴OE′=OF′，
∵∠F′OB=∠E′OA，OA=OB，
在△E′AO和△F′BO中，
$\left\{\begin{array}{l}{OE′=OF′}\\{∠F′OB=∠E′OA}\\{OA=OB}\end{array}\right.$
∴△E′AO≌△F′BO，
∴AE′=BF′；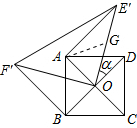  
（2）证明：∵取OE′中点G，连接AG，
∵∠AOD=90°，α=30°，
∴∠E′OA=90°-α=60°，
∵OE′=2OA，
∴OA=OG，
∴∠E′OA=∠AGO=∠OAG=60°，
∴AG=GE′，
∴∠GAE′=∠GE′A=30°，
∴∠E′AO=90°，
∴△AOE′为直角三角形．

点评 本题考查了正方形的性质，利用正方形的特殊性质求解．本题结合了三角形全等并且涉及到探究性的问题，综合性较强．对基本的知识点有很清楚的认识并熟练掌握是解决问题的关键．