

分析 (1)结论:PD=PE.如图②中,连接PC.只要证明△DPC≌△EPB,即可解决问题.
(2)不可能.理由:∠PBE=45°或135°.
解答 解:(1)结论:PD=PE.
理由:如图②中,连接PC.
∵∠C=90°,AC=BC,AP=PB,
∴PC=PA=PB,CP⊥AB,∠PCA=∠PCB=∠B=45°,
∵∠DPE=∠CPB=90°,
∴∠DPC=∠EPB,
在△DPC和△EPB中,
$\left\{\begin{array}{l}{∠DPC=∠EPB}\\{∠DCP=∠B}\\{PC=PB}\end{array}\right.$,
∴△DPC≌△EPB,
∴PD=PE.
(2))△PBE不可能是等边三角形.
利用:∵△ABC是等腰直角三角形,
∴∠PBE=45°或135°,
∴△PBE不可能是等边三角形.
点评 本题考查旋转变换、等腰直角三角形的性质、全等三角形的判定和性质,解题的关键是熟练掌握全等三角形的判定和性质,属于基础题,中考常考题型.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:解答题
| 坡度 | 1:20 | 1:16 | 1:12 |
| 最大高度(米) | 1.50 | 1.00 | 0.75 |
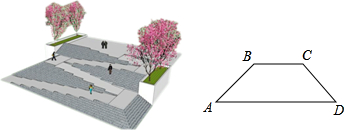
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在楼房底部B处看热气球底部A处的仰角为60°,同时在这栋楼的顶部C处看A处的仰角为30°,已知楼高BC为30m,求此时热气球底部A处的高度.(测角仪的高度忽略不计)
如图,在楼房底部B处看热气球底部A处的仰角为60°,同时在这栋楼的顶部C处看A处的仰角为30°,已知楼高BC为30m,求此时热气球底部A处的高度.(测角仪的高度忽略不计)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
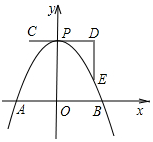 如图,一条抛物线与x轴的交点为A、B两点,其顶点P在折线C-D-E上运动.若C、D、E的坐标分别为(-1,4)、(3、4)、(3,1),点B横坐标的最小值为1,则点A横坐标的最大值为2.
如图,一条抛物线与x轴的交点为A、B两点,其顶点P在折线C-D-E上运动.若C、D、E的坐标分别为(-1,4)、(3、4)、(3,1),点B横坐标的最小值为1,则点A横坐标的最大值为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
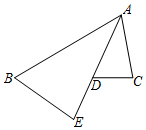 如图,已知AE 平分∠BAC,$\frac{AB}{AE}$=$\frac{AD}{AC}$.
如图,已知AE 平分∠BAC,$\frac{AB}{AE}$=$\frac{AD}{AC}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com