
【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下: ∵∠1=∠2(已知),
且∠1=∠CGD()
∴∠2=∠CGD(等量代换)
∴CE∥BF()
∴∠=∠BFD()
又∵∠B=∠C(已 知)
∴(等量代换)
∴AB∥CD()
【答案】(对顶角相等);(同位角相等,两直线平行);C;(两直线平行,同位角相等);∠BFD=∠B;(内错角相等,两直线平行)
【解析】解:∵∠1=∠2(已知), 且∠1=∠CGD(对顶角相等),
∴∠2=∠CGD(等量代换),
∴CE∥BF(同位角相等,两直线平行),
∴∠C=∠BFD(两直线平行,同位角相等),
又∵∠B=∠C(已知),
∴∠BFD=∠B(等量代换),
∴AB∥CD(内错角相等,两直线平行).
所以答案是:(对顶角相等),(同位角相等,两直线平行),C,(两直线平行,同位角相等),(内错角相等,两直线平行)
【考点精析】掌握平行线的判定与性质是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC. 
(1)求证:△BAD≌△ACE;
(2)若∠B=30°,AB=26,BD=10,求平行四边形ABDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列单项式按以下规律排列:a,3a2 , 5a3 , 7a,9a2 , 11a3 , 13a,…,则第2016个单项式应是( )
A.4031a3
B.4031a
C.4031a2
D.4032a3
查看答案和解析>>
科目:初中数学 来源: 题型:
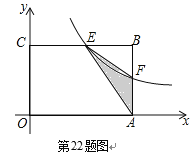
【题目】(本题满分8分)
如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数![]() 的图象与BC边交于点E.
的图象与BC边交于点E.
⑴当F为AB的中点时,求该函数的解析式;
⑵当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要使多项式(x2+px+2)(x﹣q)不含关于x的二次项,则p与q的关系是( )
A. 相等 B. 互为相反数 C. 互为倒数 D. 乘积为﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com