
 如图所示,?ABCD中,AE、CF分别平分∠BAD,∠BCD交DC、BA的延长线于E、F,求证:∠E=∠F.
如图所示,?ABCD中,AE、CF分别平分∠BAD,∠BCD交DC、BA的延长线于E、F,求证:∠E=∠F. 分析 利用平行四边形的性质进而得出AB=BG,同理可得出:CD=HD,即可得出四边形AGCH是平行四边形,进而四边形AFCE是平行四边形,所以可证明∠E=∠F.
解答 证明:∵在?ABCD中,
∴∠BAD=∠BCD,AD∥BC,AB∥CD,AD=BC,AB=CD,
∵∠BAD,∠BCD的平分线AF、CE分别交DC、BA的延长线于点F、E,
∴∠BAG=∠DAG=∠BCH=∠DCH,
∵AD∥BC,
∴∠DAG=∠AFB,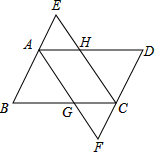
∴∠BAG=∠BGA,
∴AB=BG,同理可得出:CD=HD,
∴HD=BG,
∴AH=CG,
又∵AH∥CG,
∴四边形AGCH是平行四边形,
∴AG∥CH,
∵AE∥CF,
∴四边形AFCE是平行四边形,
∴∠E=∠F.
点评 此题主要考查了平行四边形的判定与性质,得出四边形AFCE是平行四边形是解题关键.


科目:初中数学 来源: 题型:解答题
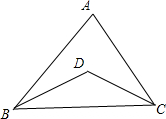 如图,BD,CD分别是△ABC的内角∠ABC、∠ACB的平分线,请说明∠BDC与∠A之间的等量关系是∠BDC=90°+$\frac{1}{2}$∠A.
如图,BD,CD分别是△ABC的内角∠ABC、∠ACB的平分线,请说明∠BDC与∠A之间的等量关系是∠BDC=90°+$\frac{1}{2}$∠A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在雷达探测到的区域,可从建立平面直角坐标系来表示位置,在某次行动中,当我方两架飞机在A(-1,2)和B(3,2)的位置,可疑飞机在C(-1,-3)的位置,你能找出这个平面直角坐标系的横、纵坐标的轴的位置吗?把它们画出来,并确定可疑飞机的位置.
在雷达探测到的区域,可从建立平面直角坐标系来表示位置,在某次行动中,当我方两架飞机在A(-1,2)和B(3,2)的位置,可疑飞机在C(-1,-3)的位置,你能找出这个平面直角坐标系的横、纵坐标的轴的位置吗?把它们画出来,并确定可疑飞机的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com