Question

如图，AB是⊙O的直径，点E是上的一点，∠DBC=∠BED．

（1）求证：BC是⊙O的切线；

（2）已知AD=3，CD=2，求BC的长．

 

 

Answer 1

(1)证明见解析

(2)BC=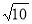

【解析】

试题分析：（1）由直径所对的圆周角是直角可得∠ADB=90°，从而可得∠BAD+∠ABD=90°，由圆周角定理可得∠BAD=∠DEC及已知可得∠ABC=90°，即BC是⊙O的切线；

（2）由已知可得△ABC∽△BDC，利用对应边成比例即可求出BC的长．

试题解析：（1）∵AB是⊙O的切直径，

∴∠ADB=90°，

又∵∠BAD=∠BED，∠BED=∠DBC，

∴∠BAD=∠DBC，

∴∠BAD+∠ABD=∠DBC+ABD=90°，

∴∠ABC=90°，

∴BC是⊙O的切线；

（2)∵∠BAD=∠DBC，∠C=∠C，

∴△ABC∽△BDC，

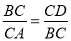∴，即BC2=AC•CD=（AD+CD）•CD=10，

∴BC=．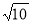

考点：1、圆周角定理；2、切线的判定；3、相似三角形的判定与性质．