
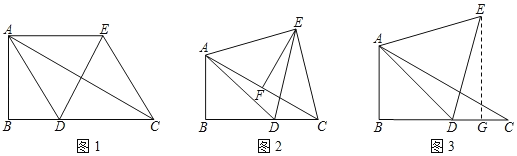
【题目】已知:在Rt△ABC中,∠B=90°,∠ACB=30°,点D为BC边上一动点,以AD为边,在AD的右侧作等边三角形ADE.
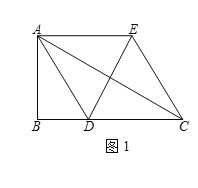
(1)当AD平分∠BAC时,如图1,四边形ADCE是 形;
(2)过E作EF⊥AC于F,如图2,求证:F为AC的中点;
(3)若AB=2,
①当D为BC的中点时,过点E作EG⊥BC于G,如图3,求EG的长;
②点D从B点运动到C点,则点E所经过路径长为 .(直接写出结果)
【答案】(1)菱形;(2)证明见解析;(3)①EG![]() ;②2
;②2![]() .
.
【解析】
(1)根据平行四边形的判定定理得到四边形ADCE为平行四边形,证明AD=AE,根据菱形的判定定理证明结论;
(2)证明△BAD≌△FAE,根据全等三角形的性质得到AB=AF,根据直角三角形的性质得到AC=2AB,证明结论;
(3)①作EF⊥AC于F,连接EC,根据勾股定理求出BC,根据等腰三角形的性质求出CG,根据勾股定理计算,得到答案; ②根据线段垂直平分线的判定定理得到E'E'垂直平分AC,证明△E'AE'≌△BAC,得到E'E'=BC=![]() .
.
解:(1)在Rt△ABC中,∠B=90°,∠ACB=30°,
∴∠BAC=60°.
∵AD平分∠BAC,
∴∠BAD=∠DAC=30°.
∵△ADE为等边三角形,
∴∠DAE=60°,
∴∠EAC=30°,
∴∠EAC=∠ACB,∠DAC=∠ACB,
∴AE∥DC,AD=DC.
∵AE=AD,∴AE=CD,
∴四边形ADCE为平行四边形.
∵AD=AE,
∴平行四边形ADCE为菱形.
故答案为:菱形;
(2)![]()
![]()
在△BAD和△FAE中,
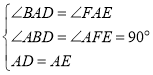 ,
,
∴△BAD≌△FAE(AAS),
∴AB=AF,
在Rt△ABC中,∠B=90°,∠ACB=30°,
∴AC=2AB,
∴AC=2AF,
∴F为AC的中点;
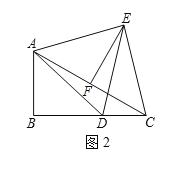
(3)①如图3,作EF⊥AC于F,连接EC,
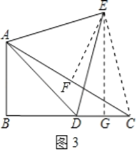
在Rt△ABC中,∠B=90°,∠ACB=30°,
∴AC=2AB=4,
∴BC![]() 2
2![]() ,
,
∵D为BC的中点,
∴BD![]() BC
BC![]() ,
,
∴AD![]() ,
,
∵AF=FC,EF⊥AC,
∴EC=AE=AD![]() ,
,
∵EC=EA=ED,EG⊥DC,
∴CG![]() CD
CD![]() ,
,
∴EG![]() ;
;
②如图4,当点D与点B重合时,点E在E'处,点E'是AC中点;
当点D与点C重合时,点E在E'处,其中△ACE'是等边三角形,
由(1)得:AE=CE,∴点E始终落在线段AC的垂直平分线上,
∴E'E'垂直平分AC,
∴点E的运动路径是从AC的中点E',沿着AC垂直平分线运动到E'处,
在△E'AE'和△BAC中,
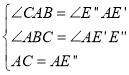 ,
,
∴△E'AE'≌△BAC(AAS),
∴E'E'=BC=2![]() .
.
故答案为:2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
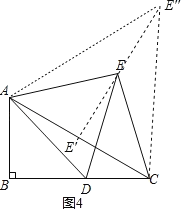
【题目】正方形![]() 的顶点
的顶点![]() ,点
,点![]() ,反比例函数
,反比例函数![]()
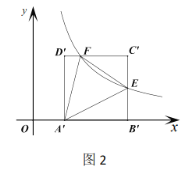
(1)如图1,双曲线经过点![]() 时求反比例函数
时求反比例函数![]() 的关系式;
的关系式;
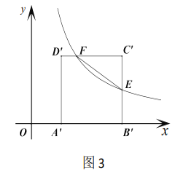
(2)如图2,正方形![]() 向下平移得到正方形
向下平移得到正方形![]() 边
边![]() 在
在![]() 轴上,反比例函数
轴上,反比例函数![]() 的图象分别交正方形
的图象分别交正方形![]() 的边
的边![]() 、边
、边![]() 于点
于点![]()
①求![]() 的面积;
的面积;
②如图3,![]() 轴上一点
轴上一点![]() ,是否存在
,是否存在![]() 是等腰三角形,若存在直接写出点
是等腰三角形,若存在直接写出点![]() 坐标,若不存在请说明理由.
坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
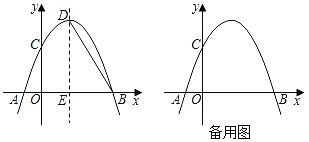
(1)求抛物线的解析式及点D的坐标;
(2)点F是抛物线上的动点,当∠FBA=2∠BDE时,求点F的坐标;
(3)若点P是x轴上方抛物线上的动点,以PB为边作正方形PBGH,随着点P的运动,正方形的大小、位置也随着改变,当顶点G或H恰好落在y轴上时,请直接写出点P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017江西省)如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)

查看答案和解析>>
科目:初中数学 来源: 题型:
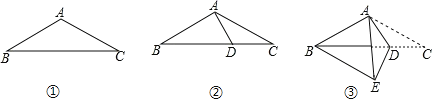
【题目】如图①,在等腰三角形ABC中,AB=AC=8,BC=14.如图②,在底边BC上取一点D,连结AD,使得∠DAC=∠ACD.如图③,将△ACD沿着AD所在直线折叠,使得点C落在点E处,连结BE,得到四边形ABED.则BE的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,连结EB,交OD于点F.
(1)求证:OD⊥BE;
(2)若DE=![]() ,AB=10,求AE的长;
,AB=10,求AE的长;
(3)若△CDE的面积是△OBF面积的![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=﹣![]() x+m(m为常数)的图象与x轴交于A(﹣3,0),与y轴交于点C.以直线x=﹣1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a>0)经过A,C两点,与x轴正半轴交于点B.
x+m(m为常数)的图象与x轴交于A(﹣3,0),与y轴交于点C.以直线x=﹣1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a>0)经过A,C两点,与x轴正半轴交于点B.
(1)求一次函数及抛物线的函数表达式;
(2)P为线段AC上的一个动点(点P与C、A不重合)过P作x轴的垂线与这个二次函数的图象交于点D,连接CD,AD,点P的横坐标为n,当n为多少时,△CDA的面积最大,最大面积为多少?
(3)在对称轴上是否存在一点E,使∠ACB=∠AEB?若存在,求点E的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com