
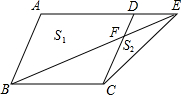
 如图,在?ABCD中,点E在边AD的延长线上,连结BE,交边DC于点F,设四边形ABFD的面积为S1,△CEF的面积为S2,若?ABCD的面积为4,则S1-S2的值为( )
如图,在?ABCD中,点E在边AD的延长线上,连结BE,交边DC于点F,设四边形ABFD的面积为S1,△CEF的面积为S2,若?ABCD的面积为4,则S1-S2的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由平行四边形的性质和已知条件得出△BCE的面积=$\frac{1}{2}$?ABCD的面积=2,△BCF的面积=4-S1,由△BCE的面积=△BCF的面积+△CEF的面积,得出2=4-S1+S2,即可得出结果.
解答 解:∵?ABCD的面积为4,四边形ABFD的面积为S1,△CEF的面积为S2,
∴△BCE的面积=$\frac{1}{2}$?ABCD的面积=2,△BCF的面积=4-S1,
∵△BCE的面积=△BCF的面积+△CEF的面积,
∴2=4-S1+S2,
∴S1-S2=2,
故选:B.
点评 本题考查了平行四边形的性质、三角形面积的计算;熟练掌握平行四边形的性质,得出三角形之间的面积关系是解决问题的关键.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:选择题
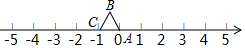 等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和-1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1;则翻转2015次后,点B所对应的数是( )
等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和-1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1;则翻转2015次后,点B所对应的数是( )| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
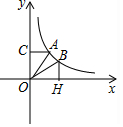 如图,点A(2,m),B(n,2),均在双曲线y=$\frac{6}{x}$(x>0)上,过点A,B分别作AG⊥y轴,BH⊥x轴,垂足为G,H,下列说法错误的是( )
如图,点A(2,m),B(n,2),均在双曲线y=$\frac{6}{x}$(x>0)上,过点A,B分别作AG⊥y轴,BH⊥x轴,垂足为G,H,下列说法错误的是( )| A. | AO=BO | B. | ∠AOB可能等于30° | ||
| C. | △AOG与△BOH的面积相等 | D. | △AOG≌△BOH |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
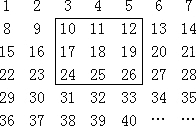 把2015个正整数1,2,3,4,…,2015按如图所示的方式排列成一个表.用一个方框按如图所示的方式任意框住9个数.
把2015个正整数1,2,3,4,…,2015按如图所示的方式排列成一个表.用一个方框按如图所示的方式任意框住9个数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
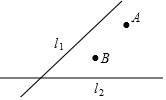 “西气东输”是造福子孙后代的创世工程,现有两条高速公路L1、L2和两个城镇A,B,准备建一个燃气控制中心站P,使中心站到两条公路距离相等,并且到两个城镇等距离,请你画出中心站的位置.(保留画图痕迹,不写画法)
“西气东输”是造福子孙后代的创世工程,现有两条高速公路L1、L2和两个城镇A,B,准备建一个燃气控制中心站P,使中心站到两条公路距离相等,并且到两个城镇等距离,请你画出中心站的位置.(保留画图痕迹,不写画法)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com