
【题目】如图,在等腰△ABC中,∠ACB = 90,点D为CB延长线上一点,过A作AE⊥AD,且AE = AD,BE与AC的延长线交于点P,求证:PB = PE.

【答案】证明见解析.
【解析】
作EM⊥AP于M,证△BCP≌△EMP,求出BC=AC=EM,证△ADC≌△EAM,推出即可;
法1:过E作EF⊥AC,垂足为F,连接BF,CE
∵ AE⊥AD,ACB = 90
∴ EAF + CAD = 90,D + CAD = 90
∴ EAF = D
又∵ AFE = ACB = 90,AE = AD
∴ △AFE ≌△DCA(AAS)
∴ EF=AC=BC
∵ BC⊥AC,EF⊥AC
∴ EF∥BC
∴ EF![]() BC
BC
∴ 四边形BCEF为平行四边形
∴ PB = PE.
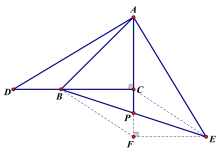
法2:∵ AD = AE且AD⊥AE
∴ 可将△ADB绕点A逆时针旋转90至△AEH,
由旋转性质得AH = AB且AH⊥AB
∴ △BAH为等腰直角三角形,ABH = 45
又∵ △ACB中,ACB = 90,AC = BC
∴ ABC = 45
∴ ABH = ABC,则B、C、H三点共线
∴ AP垂直平分BH
∴ PH = PB
∴ PBH = PHB
又由旋转性质得EH⊥BD,即EH⊥BH
∴ PHE = 90-PHB,PEH = 90-PBH,
∴ PEH = PHB
∴ PH=PE
∴ PB=PE


科目:初中数学 来源: 题型:
【题目】有甲、乙、丙三种糖果混合而成的什锦糖100千克,其中各种糖果的单价和千克数如表所示,商家用加权平均数来确定什锦糖的单价.
甲种糖果 | 乙种糖果 | 丙种糖果 | |
单价(元/千克) | 15 | 25 | 30 |
千克数 | 40 | 40 | 20 |
(1)求该什锦糖的单价.
(2)为了使什锦糖的单价每千克至少降低2元,商家计划在什锦糖中加入甲、丙两种糖果共100千克,问其中最多可加入丙种糖果多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,﹣4),B(3,﹣2),C(6,﹣3).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2 , 使△A2B2C2与△A1B1C1的相似比为2:1;
(3)若每一个方格的面积为1,则△A2B2C2的面积为 . 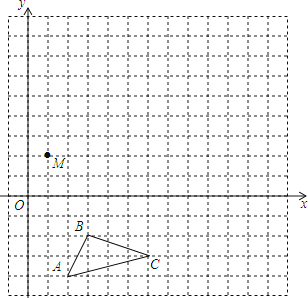
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对一大型超市销售的甲、乙、丙3种大米进行质量检测.共抽查大米200袋,质量评定分为A、B两个等级(A级优于B级),相应数据的统计图如下: 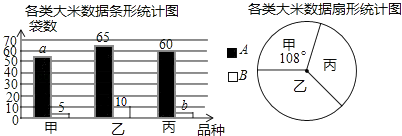
根据所给信息,解决下列问题:
(1)a= , b=;
(2)已知该超市现有乙种大米750袋,根据检测结果,请你估计该超市乙种大米中有多少袋B级大米?
(3)对于该超市的甲种和丙种大米,你会选择购买哪一种?运用统计知识简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( ) 
A.50°
B.60°
C.70°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表反映的是某地区电的使用量x(千瓦时)与应交电费y(元)之间的关系,下列说法不正确的是( )
用电量x(千瓦时) | 1 | 2 | 3 | 4 | … |
应交电费y(元) | 0.55 | 1.1 | 1.65 | 2.2 | … |
A. x与y都是变量,且x是自变量,y是x的函数
B. 用电量每增加1千瓦时,电费增加0.55元
C. 当交电费20.5元时,用电量为37千瓦时
D. 若用电量为8千瓦时,则应交电费4.4元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克比原来少2元,发现原来买这种水果80千克的钱,现在可买88千克. 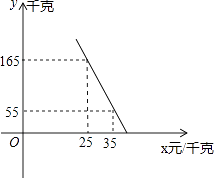
(1)现在实际购进这种水果每千克多少元?
(2)王阿姨准备购进这种水果销售,若这种水果的销售量y(千克)与销售单价x(元/千克)满足如图所示的一次函数关系. ①求y与x之间的函数关系式;
②请你帮王阿姨拿个主意,将这种水果的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入﹣进货金额)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形ABCD中,∠A=60°,点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止,点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t(s).△APQ的面积S(cm2)与t(s)之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出.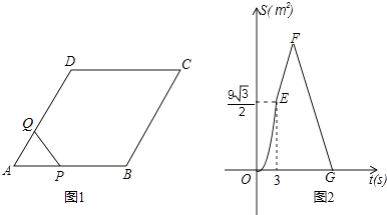
(1)求点Q运动的速度;
(2)求图2中线段FG的函数关系式;
(3)问:是否存在这样的t,使PQ将菱形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com