
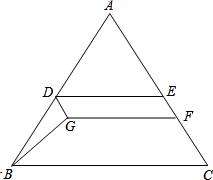
 如图:在△ABC中,AB=AC=10,sinA=$\frac{24}{25}$,点D在线段AB上以每秒1个单位长度的速度从点A向点B的方向运动(D不与A,B重合),DE∥BC交AC于点E,点F在线段EC上,且EF=$\frac{1}{4}$AE,以DE、EF为邻边构造平行四边形EFGD,连结BG
如图:在△ABC中,AB=AC=10,sinA=$\frac{24}{25}$,点D在线段AB上以每秒1个单位长度的速度从点A向点B的方向运动(D不与A,B重合),DE∥BC交AC于点E,点F在线段EC上,且EF=$\frac{1}{4}$AE,以DE、EF为邻边构造平行四边形EFGD,连结BG分析 (1)作BH⊥AC于点H,在直角△ABH中利用三角函数即可求解,证明三角形ADE是等腰三角形,则AE=AD=t,则EF即可求得;
(2)△BDG中已知BD=10-t和DG=EF,而∠BDG=∠A,利用三角形的面积公式即可求解;
(3)当△DBG是等腰三角形时,分别从BD=DG,BD=BG,DG=BG去分析求解即可求得答案.
解答 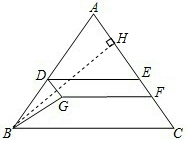 解:(1)作BH⊥AC于点H.
解:(1)作BH⊥AC于点H.
∵在Rt△ABH,sinA=$\frac{BH}{AB}$,
∴BH=AB•sinA=10×$\frac{24}{25}$=$\frac{48}{5}$.
∵DE∥BC,
∴△ADE∽△ABC,
∴AD:AC=AE:AC,
∵AB=AC,
∴AE=AD=t,
又∵EF=$\frac{1}{4}$AE,
∴EF=$\frac{1}{4}$t.
故答案是:$\frac{48}{5}$,$\frac{1}{4}$t;
(2)∵四边形DEFG是平行四边形,
∴DG=EF=$\frac{1}{4}$t,
又∵DG∥AC,
∴∠BDG=∠A,
∴S=$\frac{1}{2}$BD•DG•sin∠BDG=$\frac{1}{2}$(10-t)•$\frac{1}{4}$t•$\frac{24}{25}$,
即S=-$\frac{3}{25}$t2+$\frac{6}{5}$t(0<t<10);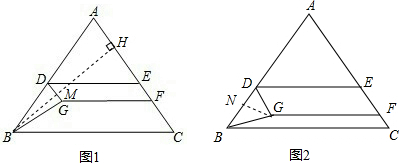 (3)若BD=DG,
(3)若BD=DG,
即10-t=$\frac{1}{4}$t,解得:t=8.
则当t=8时,△DBG是等腰三角形.
若BD=BG,则BH⊥DG于点M,
∴DM=$\frac{1}{2}$DG,
∵sin∠BDG=$\frac{24}{25}$,
∴cos∠BDG=$\frac{7}{25}$,
∵DM=BD•cos∠BDG,
∴$\frac{1}{2}$×$\frac{1}{4}$t=$\frac{7}{25}$(10-t),
解得:t=$\frac{560}{81}$;
若DG=BG,过点G作GN⊥BD于点N,
∴DN=$\frac{1}{2}$BD=DG•cos∠BDG,
∴$\frac{1}{2}$(10-t)=$\frac{7}{25}$×$\frac{1}{4}$t,
解得:t=$\frac{500}{57}$.
综上所述:当t=8或$\frac{560}{81}$或$\frac{500}{57}$时,△BDG是等腰三角形.
点评 此题属于相似三角形的综合题.考查了相似三角形的判定与性质,平行四边形的性质以及等腰三角形的性质.利用方程思想与分类讨论思想的求解是解此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,市政府准备修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的余弦值为$\frac{4}{5}$,则坡面AC的长度为10m.
如图,市政府准备修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的余弦值为$\frac{4}{5}$,则坡面AC的长度为10m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com