7．（1）在同一平面直角坐标系中，作出函数y=-2x与y=2x+4的图象．
（2）利用图象法求方程组$\left\{\begin{array}{l}2x+y=0\\ y=2x+4\end{array}\right.$的解．
分析 （1）利用两点确定一直线即可画出两一次函数图象．
（2）根据图象得出函数y=-2x与y=2x+4的图象的交点坐标为（-1，2），从而求得方程组的解
解答 解：（1）如图：
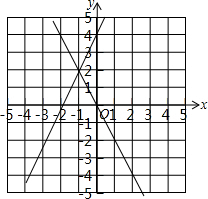
（2）根据图象可知交点无（-1，2），
所以，方程组$\left\{\begin{array}{l}2x+y=0\\ y=2x+4\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$．
点评 此题主要考查了二元一次方程组与一次函数的关系，关键是掌握方程组的解就是两函数图象的交点．
全优点练单元计划系列答案
