练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，点在边上，点为边上一动点，连接与关于所在直线对称，点分别为的中点，连接并延长交所在直线于点，连接．当为直角三角形时，的长为_________ ．

    【答案】或

    【解析】

    当△为直角三角形时，存在两种情况：

    ①当时，如图1，根据对称的性质和平行线可得：，根据直角三角形斜边中线的性质得：，最后利用勾股定理可得的长；

    ②当时，如图2，证明是等腰直角三角形，可得．

    解：当△为直角三角形时，存在两种情况：

    ①当时，如图1，

    △与关于所在直线对称，

    ，，

    点，分别为，的中点，

    、是的中位线，

    ，

    ，

    ，

    ，

    ，

    ，

    ，

    △中，是斜边的中点，

    ，

    由勾股定理得：，

    ；

    ②当时，如图2，

    ，

    ，

    △与关于所在直线对称，

    ，

    是等腰直角三角形，

    ；

    综上所述，的长为或4；

    故答案为：或4；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

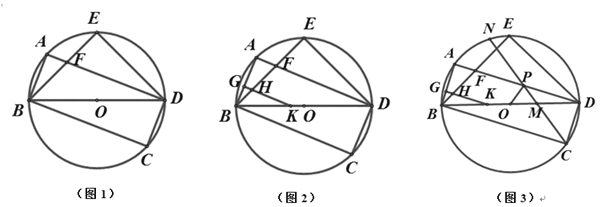
    【题目】已知：矩形ABCD内接于⊙O，连接 BD，点E在⊙O上，连接 BE交 AD于点F，∠BDC+45°=∠BFD，连接ED．

    （1）如图 1，求证：∠EBD=∠EDB；

    （2）如图2，点G是 AB上一点，过点G作 AB的垂线分别交BE和 BD于点H和点K，若HK=BG+AF，求证：AB=KG；

    （3）如图 3，在（2）的条件下，⊙O上有一点N，连接 CN分别交BD和 AD于点 M和点 P，连接 OP，∠APO=∠CPO，若 MD=8，MC= 3，求线段 GB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司生产并销售A,B两种品牌新型节能设备,第一季度共生产两种品牌设备20台,每台的成本和售价如下表:

    品牌

    A

    B

    成本价(万元/台)

    3

    5

    销售价(万元/台)

    4

    8

    设销售A种品牌设备x台,20台A,B两种品牌设备全部售完后获得利润y万元.(利润=销售价－成本)

    (1)求y关于x的函数关系式;

    (2)若生产两种品牌设备的总成本不超过80万元,那么公司如何安排生产A,B两种品牌设备,售完后获利最多?并求出最大利润;

    (3)公司为营销人员制定奖励促销政策:第一季度奖金=公司总利润销售A种品牌设备台数,那么营销人员销售多少台A种品牌设备,获得奖励最多?最大奖金数是多少?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某高级酒店为了吸引顾客，设立了一个可以自由转动的转盘，如图所示，并规定：顾客消费100以上（不包括100元），就能获得一次转动转盘的机会，如果转盘停止后，指针正好对准九折、八折、七折、五折区域顾客就可以获得此项待遇（转盘等分成16份）.

    （1）甲顾客消费80元，是否可获得转动转盘的机会？

    （2）乙顾客消费150元，获得打折待遇的概率是多少？

    （3）他获得九折，八折，七折，五折待遇的概率分别是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某旅行团计划今年暑假组织一个老年人团去昆明旅游，预定宾馆住宿时，有住宿条件一样的甲、乙两家宾馆供选择，其收费标准为每人每天120元，并且各自推出不同的优惠方案.甲家是35人（含35人）以内的按标准收费，超过35人的，超出部分按九折收费；乙家是45人（含45人）以内的按标准收费，超过45人的，超出部分按八折收费．设老年团的人数为.

    （1）根据题意，用含有的式子填写下表：

    甲宾馆收费/元

    5280

    乙宾馆收费/元

    5400

    （2）当老年人团的人数为何值时，在甲、乙两家宾馆的花费相同？如果老年人团的人数超过60人，在哪家宾馆住宿比较省钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

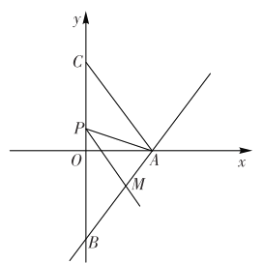
    【题目】如图，已知直线与轴交于点，与轴交于点将沿轴折叠，使点落在轴的点上，设为线段上的一个动点，点与点不重合，连接．以点为端点作射线交线段于点使．

    求点的坐标；

    当时，求直线的解析式；

    是否存在点使为直角三角形？若存在，请直接写出点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

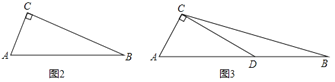
    【题目】如图，平面内的两条直线l1、l2,点A、B在直线l2上，过点A、B两点分别作直线l1的垂线，垂足分别为A1、B1，我们把线段A1B1叫做线段AB在直线l2上的正投影，其长度可记作T（AB，CD）或T（AB，l2）,特别地，线段AC在直线l2上的正投影就是线段A1C，请依据上述定义解决如下问题.

    （1）如图1，在锐角△ABC中，AB=5，T（AC，AB）=3，则T（BC，AB）= ；

    （2）如图2，在Rt△ABC中，∠ACB=90°，T（AC，AB）=4，T（BC，AB）=9，求△ABC的面积；

    （3）如图3，在钝角△ABC中，∠A=60°，点D在AB边上，∠ACD=90°，T（AD，AC）=2，T（BC，AB）=6，求T（BC，CD）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在证明定理“三角形的中位线平行于第三边，且等于第三边的一半”时，小明给出如下部分证明过程．

    已知:在中，分别是边的中点．

    求证： ．

    证明：如图，延长到点，使，连接，

    ···

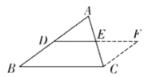
    （1）补全求证：

    （2）请根据添加的辅助线，写出完整的证明过程；

    （3）若求边的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC的边AB是⊙O的直径，点C在⊙O上，已知AC＝6cm，BC＝8cm，点P、Q分别在边AB、BC上，且点P不与点A、B重合，BQ＝kAP（k＞0），联接PC、PQ．

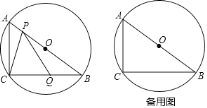
    （1）求⊙O的半径长；

    （2）当k＝2时，设AP＝x，△CPQ的面积为y，求y关于x的函数关系式，并写出定义域；

    （3）如果△CPQ与△ABC相似，且∠ACB＝∠CPQ，求k的值．

    查看答案和解析>>

    同步练习册答案