
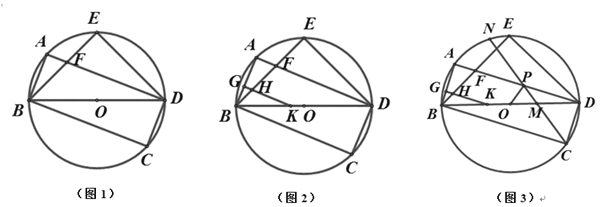
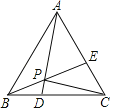
【题目】已知:矩形ABCD内接于⊙O,连接 BD,点E在⊙O上,连接 BE交 AD于点F,∠BDC+45°=∠BFD,连接ED.
(1)如图 1,求证:∠EBD=∠EDB;
(2)如图2,点G是 AB上一点,过点G作 AB的垂线分别交BE和 BD于点H和点K,若HK=BG+AF,求证:AB=KG;
(3)如图 3,在(2)的条件下,⊙O上有一点N,连接 CN分别交BD和 AD于![]() 点 M和点 P,连接 OP,∠APO=∠CPO,若 MD=8,MC= 3,求线段 GB的长.
点 M和点 P,连接 OP,∠APO=∠CPO,若 MD=8,MC= 3,求线段 GB的长.
【答案】(1)证明见解析;(2)证明见解析;(3)GB![]() .
.
【解析】
(1)根据矩形的性质可知∠BDC=∠DBA,∠A=90°,再结合已知条件∠BDC+45°=∠BFD,通过角的等量代换可得出∠EBD=45°,又因为∠BED=90°,即可得出结论;
(2)过点K 作 KS⊥BE,垂足为 R,交 AB 于点 S.证明△SRB≌△HRK,得出SB=HK,再证明△ABF≌△GKS,即可得出结论;
(3)过点 O 分别作AD 和 CN 的垂线,垂足分别为 Q 和 T,连接 OC.通过证明△OQD≌△OTC,得出AD=CN=BC,连接ON,证△NOC≌△BOC,得出∠BCO=∠NCO
设∠OBC=∠OCB=∠NCO=α,由此得出∠MOC=2α,过点 M 作 MW⊥OC,垂足为 W
在 OC 上取一点 L,使 WL=OW,连接 ML,设OM=ML=LC=a,根据勾股定理可求出OM的值,继而求出MW=3,WC=9,∴OB=OC=OD=13,BD=26,再解直角三角形即可.
解:(1)如图1,∵矩形 ABCD
∴AB∥CD,∠A=90°
∴∠BDC=∠DBA,BD是⊙O的直径
∴∠BED=90°
∵∠BFD=∠ABF+∠A,∠BFD=∠BDC+45°
∴∠ABF+∠A=∠BDC+45°
即∠ABF+90°=∠DBA+45°
∴∠DBA-∠ABF=45°
∴∠EBD=45°
∴∠EBD=∠EDB
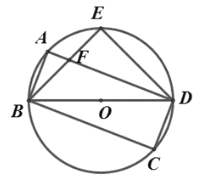
(2)证明:如下图 ,在图2中,过点K 作 KS⊥BE,垂足为 R,交 AB 于点 S.
∵KG⊥AB
∴∠BGH=∠KRH=∠SRB=∠KGS=90°
∴∠SBR=∠HKR
∵∠RBK=∠RKB=45°
∴BR=KR
∵∠SRB=∠HRK=90°
∴△SRB≌△HRK
∴SB=HK
∵SB=BG+SG,HK=BG+AF
∴BG+SG=BG+AF
∴SG=AF
∵∠ABF=∠GKS,∠BAF=∠KGS=90°
∴△ABF≌△GKS
∴AB=KG
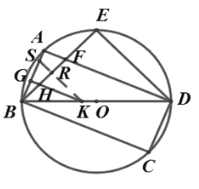
(3)如下图 ,在图3中,过点 O 分别作AD 和 CN 的垂线,垂足分别为 Q 和 T,连接 OC.
∵∠APO=∠CPO
∴OQ=OT
∵OD=OC,∠OQD=∠OTC=90°
∴△OQD≌△OTC
∴DQ=CT
∴AD=CN=BC
连接 ON
∵OC=OC,ON=OB
∴△NOC≌△BOC
∴∠BCO=∠NCO
设∠OBC=∠OCB=∠NCO=α
∴∠MOC=2α
过点 M 作 MW⊥OC,垂足为 W
在 OC 上取一点 L,使 WL=OW,连接 ML
∴MO=ML
∴∠MOL=∠MLO=2α
∴∠LCM=∠LMC=α
∴ML=CL
设OM=ML=LC=a
则OD=a+8=OC,∴OL=8,OW=WL=4
∵OM 2OW2MW2MC 2CW 2
∴ ![]()
![]() (9 舍去),
(9 舍去),![]() 5
5
∴OM=5
∴MW=3,WC=9,∴OB=OC=OD=13,BD=26
∵∠GKB=∠CBD=∠ADB=∠BCO=∠MCW,tan∠MCW=![]()
∴tan∠GKB=tan∠CBD=tan∠ADB=tan∠BCO=tan∠MCW=![]()
∴CD=GK=AB![]()
在 Rt△GKB 中,tan∠GKB= ![]()
∴GB![]()


科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.

(1)求二次函数的解析式和直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() ,当点
,当点![]() 在第一象限时,求线段
在第一象限时,求线段![]() 长度的最大值;
长度的最大值;
(3)在抛物线上是否存在异于![]() 的点
的点![]() ,使
,使![]() 中
中![]() 边上的高为
边上的高为![]() ,若存在求出点
,若存在求出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,等边△ABC的边长为4,点D是BC边上一动点,且CE=BD,连接AD,BE,AD与BE相交于点P,连接PC.则线段PC的最小值等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() :
:![]() 与直线
与直线![]() 分别交于点
分别交于点![]() .直线
.直线![]() 与
与![]()
![]()
![]() 交于点
交于点![]() .记线段
.记线段![]() ,
,![]() 围成的区域(不含边界)为
围成的区域(不含边界)为![]() .横,纵坐标都是整数的点叫做整点.
.横,纵坐标都是整数的点叫做整点.
(1)当![]() 时,区域
时,区域![]() 内的整点个数为_____;
内的整点个数为_____;
(2)若区域![]() 内没有整点,则
内没有整点,则![]() 的取值范围是_______.
的取值范围是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
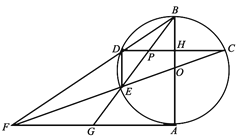
【题目】如图,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 的一条弦,
的一条弦,![]() ,
,![]() 的延长线交⊙
的延长线交⊙![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,且恰好
,且恰好![]() ∥
∥![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)求证:点![]() 是
是![]() 的中点;
的中点;
(3)当⊙![]() 的半径为
的半径为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)
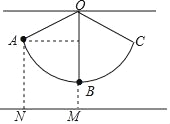
【答案】15cm
【解析】
试题设细线OB的长度为xcm,作AD⊥OB于D,证出四边形ANMD是矩形,得出AN=DM=14cm,求出OD=x-9,在Rt△AOD中,由三角函数得出方程,解方程即可.
试题解析:设细线OB的长度为xcm,作AD⊥OB于D,如图所示:
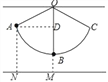
∴∠ADM=90°,
∵∠ANM=∠DMN=90°,
∴四边形ANMD是矩形,
∴AN=DM=14cm,
∴DB=14﹣5=9cm,
∴OD=x﹣9,
在Rt△AOD中,cos∠AOD=![]() ,
,
∴cos66°=![]() =0.40,
=0.40,
解得:x=15,
∴OB=15cm.
【题型】解答题
【结束】
20
【题目】已知:如图,在半径为![]() 的
的![]() 中,
中,![]() 、
、![]() 是两条直径,
是两条直径,![]() 为
为![]() 的中点,
的中点,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,且
,且![]() ,连接
,连接![]() 。
。![]() .
.
(1)求证:![]() ;
;
(2)求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
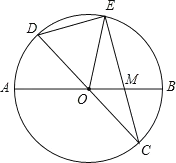
【题目】△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
(1)如图(a)所示,当点D在线段BC上时.
①求证:△AEB≌△ADC;
②探究四边形BCGE是怎样特殊的四边形?并说明理由;
(2)如图(b)所示,当点D在BC的延长线上时,直接写出(1)中的两个结论是否成立;
(3)在(2)的情况下,当点D运动到什么位置时,四边形BCGE是菱形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将![]() 放在每个小正方形的边长为1的网格中,点
放在每个小正方形的边长为1的网格中,点![]() ,点
,点![]() ,点
,点![]() 均落在格点上.
均落在格点上.
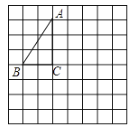
(1)![]() _________.
_________.
(2)请在如图所示的网格中,用无刻度的直尺,画出一个以![]() 为底边的等腰
为底边的等腰![]() ,使该三角形的面积等于
,使该三角形的面积等于![]() 的面积,并简要说明点
的面积,并简要说明点![]() 的位置是如何找到的(不要求证明)__________.
的位置是如何找到的(不要求证明)__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
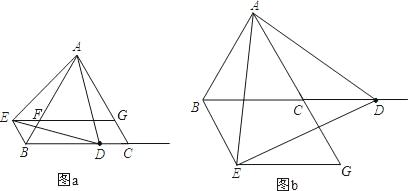
【题目】如图,![]() 点
点![]() 在边
在边![]() 上,
上,![]() 点
点![]() 为边
为边![]() 上一动点,连接
上一动点,连接![]() 与
与![]() 关于
关于![]() 所在直线对称,点
所在直线对称,点![]() 分别为
分别为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .当
.当![]() 为直角三角形时,
为直角三角形时,![]() 的长为_________ .
的长为_________ .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com