
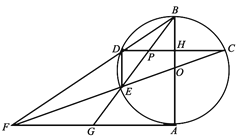
【题目】如图,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 的一条弦,
的一条弦,![]() ,
,![]() 的延长线交⊙
的延长线交⊙![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,且恰好
,且恰好![]() ∥
∥![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)求证:点![]() 是
是![]() 的中点;
的中点;
(3)当⊙![]() 的半径为
的半径为![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() =
=![]() .
.
【解析】
(1)根据![]() ∥
∥![]() ,
,![]() 可证FA⊥AB,则可得
可证FA⊥AB,则可得![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)连接![]() ,易证△GEA∽△GAB,可得
,易证△GEA∽△GAB,可得![]() ,根据
,根据![]() ∥
∥![]() ,可得
,可得![]() ,即有
,即有![]() ,可证点
,可证点![]() 是
是![]() 的中点;
的中点;
(3)利用![]() ∥
∥![]() ,得:
,得:![]() ,易证DE=BH,根据点O是CE中点,点H是CD的中点,得
,易证DE=BH,根据点O是CE中点,点H是CD的中点,得![]() ,有OH=2,CH=
,有OH=2,CH=![]() ,可求得
,可求得![]() =tan∠OCH =
=tan∠OCH =![]() .
.
(1)证明:∵![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 的一条弦,
的一条弦,![]()
∴AB⊥CD,又![]() ∥
∥![]() ,
,
∴FA⊥AB,
∴![]() 是⊙
是⊙![]() 的切线.
的切线.
(2)证明:连接![]() ,
,

∵![]() 是⊙
是⊙![]() 的直径,
的直径,
∴AE⊥BG.又FA⊥AB,
∴∠GEA=∠GAB,
又∵∠GBA=∠ABG.
∴△GEA∽△GAB,
∴![]()
![]()
∵![]() ∥
∥![]() ,
,
∴∠C=∠EFG,又∠C=∠FBE.
∴∠EFG=∠FBG,又∠FGE=∠BGF.
∴△EFG∽△FBG,
∴![]()
![]()
![]() ,
,
![]()
∴点![]() 是
是![]() 的中点;
的中点;
(3)解:∵![]() ∥
∥![]() ,∴
,∴![]() .
.
又∵GF=GA,∴DP=HP.
又∵CE是⊙![]() 的直径,D在圆上∴CD⊥DE,
的直径,D在圆上∴CD⊥DE,
又∵AB⊥CD于点H,
∴点H是CD的中点,AB∥DE,
又∵DP=HP,
∴DE=BH,
又∵点O是CE中点,点H是CD的中点,
∴![]()
又∵⊙![]() 的半径为6,
的半径为6,
∴OH=2,CH=![]() ,
,
∴![]() =tan∠OCH =
=tan∠OCH =![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣x2+4x+5图象的顶点为D,对称轴是直线1,一次函数y![]() x+1的图象与x轴交于点A,且与直线DA关于l的对称直线交于点B.
x+1的图象与x轴交于点A,且与直线DA关于l的对称直线交于点B.
(1)点D的坐标是 ;
(2)直线l与直线AB交于点C,N是线段DC上一点(不与点D、C重合),点N的纵坐标为n.过点N作直线与线段DA、DB分别交于点P、Q,使得△DPQ与△DAB相似.
①当n![]() 时,求DP的长;
时,求DP的长;
②若对于每一个确定的n的值,有且只有一个△DPQ与△DAB相似,请直接写出n的取值范围 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 交于点
交于点![]() ,将点
,将点![]() 向右平移某个距离得到点
向右平移某个距离得到点![]() ,点
,点![]() 在抛物线上.已知点
在抛物线上.已知点![]() ,
,![]() .
.
(1) 当![]() 时.
时.
①求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
②求线段![]() 的长度;
的长度;
(2)若抛物线与线段![]() 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
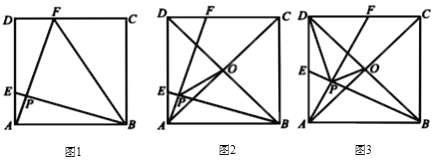
【题目】如图,在正方形![]() 中,
中,![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
(1)如图1,连接![]() ,当
,当![]() ,
,![]() 时,求
时,求![]() 的长;
的长;
(2)如图2,对角线![]() ,
,![]() 交于点
交于点![]() .连接
.连接![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)如图3,对角线![]() ,
,![]() 交于点
交于点![]() .连接
.连接![]() ,
,![]() ,若
,若![]() ,试探索
,试探索![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
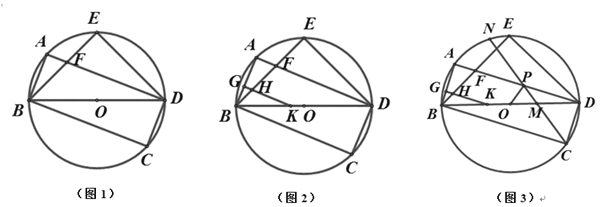
【题目】已知:矩形ABCD内接于⊙O,连接 BD,点E在⊙O上,连接 BE交 AD于点F,∠BDC+45°=∠BFD,连接ED.
(1)如图 1,求证:∠EBD=∠EDB;
(2)如图2,点G是 AB上一点,过点G作 AB的垂线分别交BE和 BD于点H和点K,若HK=BG+AF,求证:AB=KG;
(3)如图 3,在(2)的条件下,⊙O上有一点N,连接 CN分别交BD和 AD于![]() 点 M和点 P,连接 OP,∠APO=∠CPO,若 MD=8,MC= 3,求线段 GB的长.
点 M和点 P,连接 OP,∠APO=∠CPO,若 MD=8,MC= 3,求线段 GB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏北五市联合通过网络投票选出了一批“最有孝心的美少年”.根据各市的入选结果制作出如下统计表,后来发现,统计表中前三行的所有数据都是正确的,后两行中有一个数据是错误的.请回答下列问题:
(1)统计表![]() ________,
________,![]() ________;
________;
(2)统计表后三行中哪一个数据是错误的?该数据的正确值是多少?
(3)组委会决定从来自宿迁市的4位“最有孝心的美少年”中,任选两位作为苏北五市形象代言人,![]() 、
、![]() 是宿迁市“最有孝心的美少年”中的两位,问
是宿迁市“最有孝心的美少年”中的两位,问![]() 、
、![]() 同时入选的概率是多少?并请画出树状图或列出表格.
同时入选的概率是多少?并请画出树状图或列出表格.
区域 | 频数 | 频率 |
宿迁 | 4 | a |
连云港 | 7 | 0.175 |
淮安 |
| 0.2 |
徐州 | 10 | 0.25 |
盐城 | 12 | 0.275 |
查看答案和解析>>
科目:初中数学 来源: 题型:
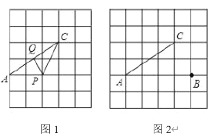
【题目】在每个小正方形的边长为1的网格中,点![]() ,
,![]() ,
,![]() 均在格点上,点
均在格点上,点![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点.
上的动点.
(I)如图(1),当点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点时,
中点时,![]() 的值为__________;
的值为__________;
(Ⅱ)当![]() 取得最小值时,在如图(2)所示的网格中,用无刻度的真尺,画出线段
取得最小值时,在如图(2)所示的网格中,用无刻度的真尺,画出线段![]() ,
,![]() ,简要说明点
,简要说明点![]() 和点
和点![]() 的位置是如何找到的(不要求证明)__________.
的位置是如何找到的(不要求证明)__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行团计划今年暑假组织一个老年人团去昆明旅游,预定宾馆住宿时,有住宿条件一样的甲、乙两家宾馆供选择,其收费标准为每人每天120元,并且各自推出不同的优惠方案.甲家是35人(含35人)以内的按标准收费,超过35人的,超出部分按九折收费;乙家是45人(含45人)以内的按标准收费,超过45人的,超出部分按八折收费.设老年团的人数为![]() .
.
(1)根据题意,用含有![]() 的式子填写下表:
的式子填写下表:
|
|
|
| |
甲宾馆收费/元 |
| 5280 | ||
乙宾馆收费/元 |
|
| 5400 |
(2)当老年人团的人数为何值时,在甲、乙两家宾馆的花费相同?如果老年人团的人数超过60人,在哪家宾馆住宿比较省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com