
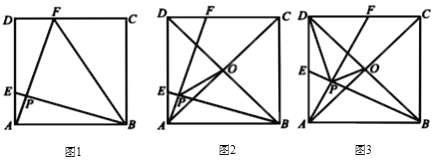
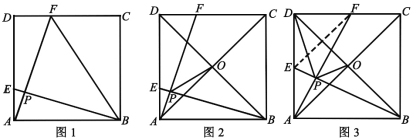
【题目】如图,在正方形![]() 中,
中,![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
(1)如图1,连接![]() ,当
,当![]() ,
,![]() 时,求
时,求![]() 的长;
的长;
(2)如图2,对角线![]() ,
,![]() 交于点
交于点![]() .连接
.连接![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)如图3,对角线![]() ,
,![]() 交于点
交于点![]() .连接
.连接![]() ,
,![]() ,若
,若![]() ,试探索
,试探索![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)BF=5;(2)![]() ;(3)
;(3)![]() ;理由见解析.
;理由见解析.
【解析】
(1)根据正方形的性质和已知条件可证明得出△ABE≌△DAF,DF=AE=1,则可得出CF的值,再根据勾股定理即可可得答案.
(2)根据正方形ABCD对角线AC,BD相交于点O,即可得出∠CAB=∠ADB=45°,∠AOB=90°,又![]() 于P,∠APB=∠AOB=90°,即A,P,O,B四点共圆,∠OPB=∠OAB=45°,∠OPB=∠ADB ,再根据∠OBP=∠DBE,即可证明得出△OPB∽△EDB,可得
于P,∠APB=∠AOB=90°,即A,P,O,B四点共圆,∠OPB=∠OAB=45°,∠OPB=∠ADB ,再根据∠OBP=∠DBE,即可证明得出△OPB∽△EDB,可得![]() ,再根据DE=2AE=4,可得AD=AB=6,BD=
,再根据DE=2AE=4,可得AD=AB=6,BD=![]() ,
,![]() ,
,![]() ,
,![]() ,即
,即![]() .
.
(3)连接EF,由(2)可得∠APB=∠AOB=90°,即A,P,O,B四点共圆,∠OPB=∠OAB=45°,∠DPE=∠OPB=45°,再根据A,P,O,B四点共圆有∠POA=∠PBA,则![]() DEP=∠DAB+∠PBA=∠AOB+∠POA=∠POB,再根据∠DPE=∠OPB证明得出△DEP∽△BOP,即
DEP=∠DAB+∠PBA=∠AOB+∠POA=∠POB,再根据∠DPE=∠OPB证明得出△DEP∽△BOP,即![]() ,再根据AF⊥BE,∠EDF=90°,得出
,再根据AF⊥BE,∠EDF=90°,得出![]() EDF+∠EPF=180°,D,E,P,F四点共圆,∠DFE=∠DPE=45°,∠DEF=∠DFE=45°,DE=DF ,又AE=DF,于是AE=DE=
EDF+∠EPF=180°,D,E,P,F四点共圆,∠DFE=∠DPE=45°,∠DEF=∠DFE=45°,DE=DF ,又AE=DF,于是AE=DE=![]() ,
,![]() ,
,![]() ,即可得出
,即可得出![]() .
.
(1)解:∵正方形ABCD.
∴∠DAB=∠D=∠C=90°,AB=BC=DC=AD=4
∵![]() 于P.
于P.
∴∠EBA+∠FAB=90°,又∠DAF+FAB=90°.
∴∠EBA=∠DAF
又∠DAB=∠D,AB=DA.
∴△ABE≌△DAF.
∴DF=AE=1,
∴CF=DC![]() DF=3
DF=3
在Rt△BFC中,![]() .
.
∴BF=5
(2)∵正方形ABCD对角线AC,BD相交于点O,
∴∠CAB=∠ADB=45°,∠AOB=90°
又![]() 于P. ∴∠APB=∠AOB=90°.
于P. ∴∠APB=∠AOB=90°.
∴A,P,O,B四点共圆. ∴∠OPB=∠OAB=45°(也可由相似证得).
∴∠OPB=∠ADB
又∠OBP=∠DBE,∴△OPB∽△EDB,可得![]()
又DE=2AE=4,可得AD=AB=6,BD=![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴![]()
(3)![]()
理由如下:连接EF.
∵![]() ,由(2)问可知∠APB=∠AOB=90° ,∴A,P,O,B四点共圆,
,由(2)问可知∠APB=∠AOB=90° ,∴A,P,O,B四点共圆,
∴∠OPB=∠OAB=45°,∴∠DPE=∠OPB=45°,
又A,P,O,B四点共圆有∠POA=∠PBA
∴![]() DEP=∠DAB+∠PBA=∠AOB+∠POA=∠POB,
DEP=∠DAB+∠PBA=∠AOB+∠POA=∠POB,
又∠DPE=∠OPB,∴△DEP∽△BOP,
∴![]()
又AF⊥BE,∠EDF=90°,∴![]() EDF+∠EPF=180°,
EDF+∠EPF=180°,
∴D,E,P,F四点共圆
∴∠DFE=∠DPE=45°,∴∠DEF=∠DFE=45°,有DE=DF
又AE=DF,于是AE=DE=![]() ,
,![]()
∴![]() ,
,
∴![]()


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴l如图所示,则下列结论:①abc>0;②a﹣b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )

A.①③ B.②③ C.②④ D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
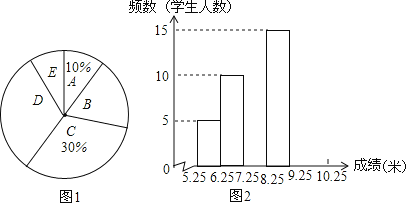
【题目】张老师抽取了九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,规定x≥6.25为合格,x≥9.25为优秀.并绘制出扇形统计图和频数分布直方图(不完整).
(1)抽取的这部分男生有______人,请补全频数分布直方图;
(2)抽取的这部分男生成绩的中位数落在_____组?扇形统计图中D组对应的圆心角是多少度?
(3)如果九年级有男生400人,请你估计他们掷实心球的成绩达到合格的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.假定每位顾客购买商品的可能性相同.
商品 顾客人数 | 甲 | 乙 | 丙 | 丁 |
100 | √ | × | √ | √ |
217 | × | √ | × | √ |
200 | √ | √ | √ | × |
300 | √ | × | √ | × |
85 | √ | × | × | × |
98 | × | √ | × | × |
(1)估计顾客同时购买乙和丙的概率为__________.
(2)如果顾客购买了甲,并且同时也在乙、丙、丁中进行了选购,则购买__________(填乙、丙、丁)商品的可能性最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面内的点![]() 和点
和点![]() ,给出如下定义:点
,给出如下定义:点![]() 为平面内一点,若点
为平面内一点,若点![]() 使得
使得![]() 是以
是以![]() 为顶角且
为顶角且![]() 小于90°的等腰三角形,则称点
小于90°的等腰三角形,则称点![]() 是点
是点![]() 关于点
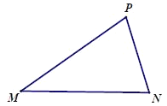
关于点![]() 的锐角等腰点.如图,点
的锐角等腰点.如图,点![]() 是点
是点![]() 关于点
关于点![]() 的锐角等腰点.
的锐角等腰点.
在平面直角坐标系xOy中,点O为坐标原点
(1)已知点![]() ,在点
,在点![]() ,
,![]() ,
,![]() ,
,![]() 中,是点
中,是点![]() 关于点
关于点![]() 的锐角等腰点的是 ;
的锐角等腰点的是 ;
(2)已知点![]() ,点
,点![]() 在直线
在直线![]() 上,若点
上,若点![]() 是点
是点![]() 关于点
关于点![]() 的锐角等腰点,求实数
的锐角等腰点,求实数![]() 的取值范围.
的取值范围.
(3) 点![]() 是
是![]() 轴上的动点,
轴上的动点,![]() ,
,![]() ,点
,点![]() 是以点
是以点![]() 为圆心,2为半径的圆上一动点.且满足
为圆心,2为半径的圆上一动点.且满足![]() ,若直线
,若直线![]() 上存在点
上存在点![]() 关于点
关于点![]() 的锐角等腰点,请直接写出
的锐角等腰点,请直接写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
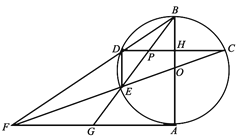
【题目】如图,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 的一条弦,
的一条弦,![]() ,
,![]() 的延长线交⊙
的延长线交⊙![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,且恰好
,且恰好![]() ∥
∥![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)求证:点![]() 是
是![]() 的中点;
的中点;
(3)当⊙![]() 的半径为
的半径为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
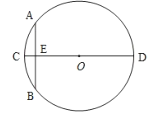
【题目】“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长六寸,问径几何?”用现代的数学语言表述是:“CD为![]() 的直径,弦
的直径,弦![]() ,垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意得CD的长为( )
,垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意得CD的长为( )
A.12寸B.13寸C.24寸D.26寸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=﹣![]() x+c与x轴交于点A(4,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(4,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过A、B两点.
x2+bx+c经过A、B两点.
(1)求抛物线表达式;
(2)点P为抛物线上的一个动点,过点P作垂直于x轴的直线分别交x轴和直线AB于M、N两点,若P、M、N三点中恰有一点是其他两点所连线段的中点(三点重合除外),请求出此时点P的坐标.
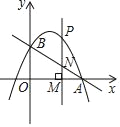
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC,∠BAC=α,直线l经过点A(不经过点B或点C),点C关于直线l的对称点为点D,连接BD,CD.
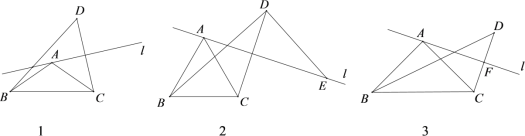
(1)如图1,
①求证:点B,C,D在以点A为圆心,AB为半径的圆上;
②直接写出∠BDC的度数(用含α的式子表示)为 ;
(2)如图2,当α=60°时,过点D作BD的垂线与直线l交于点E,求证:AE=BD;
(3)如图3,当α=90°时,记直线l与CD的交点为F,连接BF.将直线l绕点A旋转的过程中,在什么情况下线段BF的长取得最大值?若AC=2![]() a,试写出此时BF的值.
a,试写出此时BF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com