
【题目】直线y=﹣![]() x+c与x轴交于点A(4,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(4,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过A、B两点.
x2+bx+c经过A、B两点.
(1)求抛物线表达式;
(2)点P为抛物线上的一个动点,过点P作垂直于x轴的直线分别交x轴和直线AB于M、N两点,若P、M、N三点中恰有一点是其他两点所连线段的中点(三点重合除外),请求出此时点P的坐标.
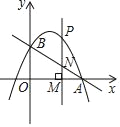
【答案】(1)抛物线解析式为y=﹣![]() +2;(2)满足条件的P点坐标为(﹣
+2;(2)满足条件的P点坐标为(﹣![]() ,
,![]() )或(﹣2,﹣3)或(1,3).
)或(﹣2,﹣3)或(1,3).
【解析】
(1)先把A点坐标代入y=-![]() x+c中求出c=2,从而得到一次函数解析式为y=-
x+c中求出c=2,从而得到一次函数解析式为y=-![]() x+2,然后把A点坐标代入y=-
x+2,然后把A点坐标代入y=-![]() x2+bx+2中求出b即可得到抛物线解析式;
x2+bx+2中求出b即可得到抛物线解析式;
(2)设P(x,-![]() x2+
x2+![]() x+2),则N(x,-
x+2),则N(x,-![]() x+2),M(x,0),讨论:当x>4时,MN=MP,则-(-
x+2),M(x,0),讨论:当x>4时,MN=MP,则-(-![]() x+2)=-
x+2)=-![]() x+2-(-
x+2-(-![]() x2+
x2+![]() x+2);当0<x<4时,PN=MN,则-
x+2);当0<x<4时,PN=MN,则-![]() x2+
x2+![]() x+2-(-
x+2-(-![]() x+2)=-
x+2)=-![]() x+2;当-1<x<0时,NP=PM,-
x+2;当-1<x<0时,NP=PM,-![]() x+2-(-
x+2-(-![]() x2+
x2+![]() x+2)=-
x+2)=-![]() x2+
x2+![]() x+2;当x<-1时,NM=PM,-
x+2;当x<-1时,NM=PM,-![]() x+2=-(-
x+2=-(-![]() x2+
x2+![]() x+2),然后分别解方程得到对应P点坐标.
x+2),然后分别解方程得到对应P点坐标.
(1)把A(4,0)代入y=﹣![]() x+c得﹣2+c=0,解得c=2,
x+c得﹣2+c=0,解得c=2,
∴一次函数解析式为y=﹣![]() x+2,
x+2,
当x=0时,y=﹣![]() x+2=2,则B(0,2),
x+2=2,则B(0,2),
把A(4,0)代入y=﹣![]() +bx+2得﹣8+4b+2=0,解得b=
+bx+2得﹣8+4b+2=0,解得b=![]() ,
,
∴抛物线解析式为y=﹣![]() +
+![]() x+2;
x+2;
(2)设P(x,﹣![]() +
+![]() x+2,则N(x,﹣
x+2,则N(x,﹣![]() x+2),M(x,0),
x+2),M(x,0),
当x>4时,MN=MP,则﹣(﹣![]() x+2)=﹣
x+2)=﹣![]() x+2﹣(﹣
x+2﹣(﹣![]() +
+![]() x+2),
x+2),
整理得x2﹣5x+4=0,解得x1=1(舍去),x2=4(舍去),
当0<x<4时,PN=MN,则﹣![]() +
+![]() x+2﹣(﹣
x+2﹣(﹣![]() x+2)=﹣
x+2)=﹣![]() x+2,
x+2,
整理得x2﹣5x+4=0,解得x1=1,x2=4(舍去),此时P(1,3);
当﹣1<x<0时,NP=PM,﹣![]() x+2﹣(﹣
x+2﹣(﹣![]() +
+![]() x +2)=﹣
x +2)=﹣![]() +
+![]() x +2
x +2
整理得2x2﹣7x﹣4=0,解得x1=﹣![]() ,x2=4(舍去),此时P(﹣
,x2=4(舍去),此时P(﹣![]() ,
,![]() );
);
当x<﹣1时,NM=PM,﹣![]() x+2=﹣(﹣
x+2=﹣(﹣![]() +
+![]() x +2),
x +2),
整理得x2﹣2x﹣8=0,解得x1=﹣2,x2=4(舍去),此时P(﹣2,﹣3);
综上所述,满足条件的P点坐标为(﹣![]() ,
,![]() )或(﹣2,﹣3)或(1,3).
)或(﹣2,﹣3)或(1,3).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为了了解某校九年级学生的课外数学学习时长情况,该校将选取部分学生进行调查,以下样本中,最具代表性的是( )
A.该年级篮球社团的学生
B.该年级数学成绩前![]() 名的女生
名的女生
C.该年级跑步较快的学生
D.从每个班级中,抽取学号为![]() 的整数倍的学生
的整数倍的学生
查看答案和解析>>
科目:初中数学 来源: 题型:
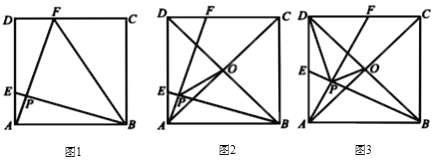
【题目】如图,在正方形![]() 中,
中,![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
(1)如图1,连接![]() ,当
,当![]() ,
,![]() 时,求
时,求![]() 的长;
的长;
(2)如图2,对角线![]() ,
,![]() 交于点
交于点![]() .连接
.连接![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)如图3,对角线![]() ,
,![]() 交于点
交于点![]() .连接
.连接![]() ,
,![]() ,若
,若![]() ,试探索
,试探索![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏北五市联合通过网络投票选出了一批“最有孝心的美少年”.根据各市的入选结果制作出如下统计表,后来发现,统计表中前三行的所有数据都是正确的,后两行中有一个数据是错误的.请回答下列问题:
(1)统计表![]() ________,
________,![]() ________;
________;
(2)统计表后三行中哪一个数据是错误的?该数据的正确值是多少?
(3)组委会决定从来自宿迁市的4位“最有孝心的美少年”中,任选两位作为苏北五市形象代言人,![]() 、
、![]() 是宿迁市“最有孝心的美少年”中的两位,问
是宿迁市“最有孝心的美少年”中的两位,问![]() 、
、![]() 同时入选的概率是多少?并请画出树状图或列出表格.
同时入选的概率是多少?并请画出树状图或列出表格.
区域 | 频数 | 频率 |
宿迁 | 4 | a |
连云港 | 7 | 0.175 |
淮安 |
| 0.2 |
徐州 | 10 | 0.25 |
盐城 | 12 | 0.275 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠C=90°,AB=10,点F是AB的中点,点D、E分别在AC、BC边上运动,且始终保持DF⊥EF,则△CDE面积的最大值为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
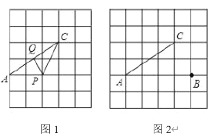
【题目】在每个小正方形的边长为1的网格中,点![]() ,
,![]() ,
,![]() 均在格点上,点
均在格点上,点![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点.
上的动点.
(I)如图(1),当点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点时,
中点时,![]() 的值为__________;
的值为__________;
(Ⅱ)当![]() 取得最小值时,在如图(2)所示的网格中,用无刻度的真尺,画出线段
取得最小值时,在如图(2)所示的网格中,用无刻度的真尺,画出线段![]() ,
,![]() ,简要说明点
,简要说明点![]() 和点
和点![]() 的位置是如何找到的(不要求证明)__________.
的位置是如何找到的(不要求证明)__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的图象与
)的图象与![]() 轴交于点
轴交于点![]() 和点
和点![]() (点
(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)用含![]() 的代数式表示点
的代数式表示点![]() 和点
和点![]() 的坐标;
的坐标;
(2)垂直于![]() 轴的直线
轴的直线![]() 在点
在点![]() 与点
与点![]() 之间平行移动,且与抛物线和直线
之间平行移动,且与抛物线和直线![]() 分别交于点
分别交于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() .
.
①当![]() 时,求
时,求![]() 的值;
的值;
②若![]() ,则当
,则当![]() 为何值时,
为何值时,![]() 取得最大值,并求出这个最大值.
取得最大值,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)求抛物线![]() 的开口方向、对称轴和顶点坐标;
的开口方向、对称轴和顶点坐标;
(2)将抛物线![]() 向下平移,得抛物线
向下平移,得抛物线![]() ,使抛物线
,使抛物线![]() 的顶点落在直线
的顶点落在直线![]() 上.
上.
①求抛物线![]() 的解析式;
的解析式;
②抛物线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),抛物线
的左侧),抛物线![]() 的对称轴于
的对称轴于![]() 轴的交点为
轴的交点为![]() ,点
,点![]() 是线段
是线段![]() 上的一点,过点
上的一点,过点![]() 作直线
作直线![]() 轴,交抛物线
轴,交抛物线![]() 于点
于点![]() ,点
,点![]() 关于抛物线对称轴的对称点为
关于抛物线对称轴的对称点为![]() ,点
,点![]() 是线段
是线段![]() 上一点,且
上一点,且![]() ,连接
,连接![]() ,作
,作![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:
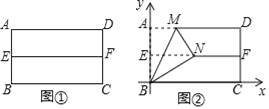
第一步:对折矩形纸片![]() ,使
,使![]() 与
与![]() 重合,得到折痕
重合,得到折痕![]() ,把纸片展开(如图①);
,把纸片展开(如图①);
第二步:再一次折叠纸片,使点![]() 落在
落在![]() 上,并使折痕经过点
上,并使折痕经过点![]() ,得到折痕
,得到折痕![]() ,同时得到线段
,同时得到线段![]() (如图②).
(如图②).
如图②所示建立平面直角坐标系,请解答以下问题:
(Ⅰ)设直线![]() 的解析式为
的解析式为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若![]() 的延长线与矩形
的延长线与矩形![]() 的边
的边![]() 交于点
交于点![]() ,设矩形的边
,设矩形的边![]() ,
,![]() ;
;
(i)若![]() ,
,![]() ,求
,求![]() 点的坐标;
点的坐标;
(ii)请直接写出![]() 、
、![]() 应该满足的条件.
应该满足的条件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com