
【题目】如图,在等腰直角△ABC中,∠C=90°,AB=10,点F是AB的中点,点D、E分别在AC、BC边上运动,且始终保持DF⊥EF,则△CDE面积的最大值为__.

【答案】![]()
【解析】
连接CF,根据全等三角形的判定定理可判定△ADF≌△CEF,设AD=x,△CDE的面积为y,则CE=x,∠C=90°,列出y关于x的二次函数,利用最值点即可得到答案.
解:如图所示,连接CF,
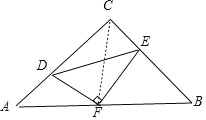
∵等腰直角△ABC中,∠C=90°,AB=10,点F是AB的中点,
∴CF=AF,∠A=∠FCE,AC=BC=10×![]() =5
=5![]() ,
,
又∵∠DFC+∠CFE=90°,∠AFD+∠CFD=90°,
∴∠AFD=∠CFE,
∴△ADF≌△CEF(ASA),
设AD=x(0<x<5![]() ),△CDE的面积为y,则CE=x,CD=5
),△CDE的面积为y,则CE=x,CD=5![]() ﹣x,∠C=90°,
﹣x,∠C=90°,
∴y=![]() x(5
x(5![]() ﹣x)=﹣
﹣x)=﹣![]() +
+![]() ,
,
即△CDE面积的最大值为![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
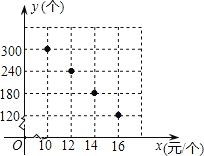
【题目】在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调査.这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:
(1)试求出y与x之间的函数关系;
(2)若许原瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面内的点![]() 和点
和点![]() ,给出如下定义:点
,给出如下定义:点![]() 为平面内一点,若点
为平面内一点,若点![]() 使得
使得![]() 是以
是以![]() 为顶角且
为顶角且![]() 小于90°的等腰三角形,则称点
小于90°的等腰三角形,则称点![]() 是点
是点![]() 关于点
关于点![]() 的锐角等腰点.如图,点
的锐角等腰点.如图,点![]() 是点
是点![]() 关于点
关于点![]() 的锐角等腰点.
的锐角等腰点.
在平面直角坐标系xOy中,点O为坐标原点
(1)已知点![]() ,在点
,在点![]() ,
,![]() ,
,![]() ,
,![]() 中,是点
中,是点![]() 关于点
关于点![]() 的锐角等腰点的是 ;
的锐角等腰点的是 ;
(2)已知点![]() ,点
,点![]() 在直线
在直线![]() 上,若点
上,若点![]() 是点
是点![]() 关于点
关于点![]() 的锐角等腰点,求实数
的锐角等腰点,求实数![]() 的取值范围.
的取值范围.
(3) 点![]() 是
是![]() 轴上的动点,
轴上的动点,![]() ,
,![]() ,点
,点![]() 是以点
是以点![]() 为圆心,2为半径的圆上一动点.且满足
为圆心,2为半径的圆上一动点.且满足![]() ,若直线
,若直线![]() 上存在点
上存在点![]() 关于点
关于点![]() 的锐角等腰点,请直接写出
的锐角等腰点,请直接写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长六寸,问径几何?”用现代的数学语言表述是:“CD为![]() 的直径,弦
的直径,弦![]() ,垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意得CD的长为( )
,垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意得CD的长为( )
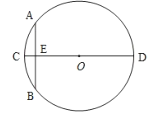
A.12寸B.13寸C.24寸D.26寸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在离水面高度(AC)为2米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米的速度收绳子.
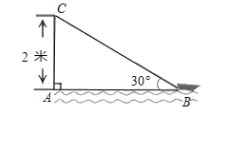
问:(1)未开始收绳子的时候,图中绳子BC的长度是多少米?
(2)收绳2秒后船离岸边多少米?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=﹣![]() x+c与x轴交于点A(4,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(4,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过A、B两点.
x2+bx+c经过A、B两点.
(1)求抛物线表达式;
(2)点P为抛物线上的一个动点,过点P作垂直于x轴的直线分别交x轴和直线AB于M、N两点,若P、M、N三点中恰有一点是其他两点所连线段的中点(三点重合除外),请求出此时点P的坐标.
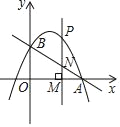
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有甲种原料![]() ,乙种原料
,乙种原料![]() ,计划用这两种原料生产
,计划用这两种原料生产![]() 、
、![]() 两种产品共40件.生产每件
两种产品共40件.生产每件![]() 种产品需甲种原料
种产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,可获利润900元;生产每件
,可获利润900元;生产每件![]() 种产品需甲种原料
种产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,可获利润1100元.设安排生产
,可获利润1100元.设安排生产![]() 种产品
种产品![]() 件(
件(![]() 为非负整数). .
为非负整数). .
(I)根据题意,填写下表:
甲( | 乙( | 件数(件) | |
|
|
| |
|
|
|
(Ⅱ) 安排生产![]() 、
、![]() 两种产品的件数有几种方案?试说明理由:
两种产品的件数有几种方案?试说明理由:
(Ⅲ) 设生产这批40件产品共可获利润![]() 元,将
元,将![]() 表示为
表示为![]() 的函数,并求出最大利润.
的函数,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
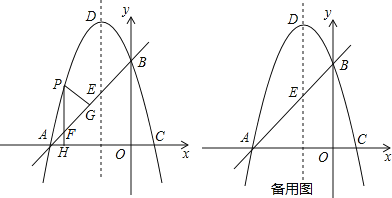
【题目】如图,在平面直角坐标系xoy中,直线y=x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线y=-x2+bx+c交x轴于另一点C,点D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)点P是直线AB上方的抛物线上一点,(不与点A、B重合),过点P作x轴的垂线交x轴于点H,交直线AB于点F,作PG⊥AB于点G.求出△PFG的周长最大值;
(3)在抛物线y=-x2+bx+c上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等?若存在,请求出此时点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
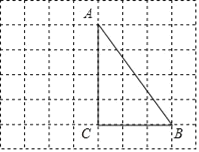
【题目】如图所示,在每个边长都为1的小正方形组成的网格中,点![]() 、
、![]() 、
、![]() 均为格点.
均为格点.
(1)线段![]() 的长度等于______;
的长度等于______;
(2)若![]() 为线段
为线段![]() 上的动点,以
上的动点,以![]() 、
、![]() 为邻边的四边形
为邻边的四边形![]() 为平行四边形,当
为平行四边形,当![]() 长度最小时,请你借助网格和无刻度的直尺画出该平行四边形,并简要说明你的作图方法:__________(不要求证明).
长度最小时,请你借助网格和无刻度的直尺画出该平行四边形,并简要说明你的作图方法:__________(不要求证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com