
【题目】某公司有甲种原料![]() ,乙种原料
,乙种原料![]() ,计划用这两种原料生产
,计划用这两种原料生产![]() 、
、![]() 两种产品共40件.生产每件
两种产品共40件.生产每件![]() 种产品需甲种原料
种产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,可获利润900元;生产每件
,可获利润900元;生产每件![]() 种产品需甲种原料
种产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,可获利润1100元.设安排生产
,可获利润1100元.设安排生产![]() 种产品
种产品![]() 件(
件(![]() 为非负整数). .
为非负整数). .
(I)根据题意,填写下表:
甲( | 乙( | 件数(件) | |
|
|
| |
|
|
|
(Ⅱ) 安排生产![]() 、
、![]() 两种产品的件数有几种方案?试说明理由:
两种产品的件数有几种方案?试说明理由:
(Ⅲ) 设生产这批40件产品共可获利润![]() 元,将
元,将![]() 表示为
表示为![]() 的函数,并求出最大利润.
的函数,并求出最大利润.
【答案】(I)![]() ,
,![]() ;(Ⅱ)共有三种方案,理由见解析;(Ⅲ) 39400.
;(Ⅱ)共有三种方案,理由见解析;(Ⅲ) 39400.
【解析】
(I)根据总件数=单件需要的原料×件数列式即可;
(Ⅱ)根据两种产品所需要的甲、乙两种原料列出不等式组,然后求解即可;
(Ⅲ)根据总利润等于两种产品的利润之和列式整理,然后根据一次函数的增减性求出最大利润即可.
(I)∵安排生产![]() 种产品
种产品![]() 件,而生产每件
件,而生产每件![]() 种产品需甲种原料
种产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,
,
∴生产![]() 种产品
种产品![]() 件,需要甲种原料为:8x,
件,需要甲种原料为:8x,
∵生产![]() 、
、![]() 两种产品共40件,
两种产品共40件,
∴生产B种产品(40-x)件,
∵生产每件![]() 种产品需乙种原料
种产品需乙种原料![]() ,
,
∴生产B种产品,需要乙种原料为:![]() ,
,
故表格分别填入:A甲种原料8x,B乙种原料9(40-x);
(Ⅱ)根据题意得,
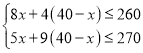
由①得,![]() ,
,
由②得,![]() ,
,
∴不等式组的解集是![]()
∵![]() 是正整数,
是正整数,
∴![]() ,
,
共有三种方案:
方案一:![]() 产品23件,
产品23件,![]() 产品17件,
产品17件,
方案二:![]() 产品24件,
产品24件,![]() 产品16件;
产品16件;
方案三:![]() 产品25件,
产品25件,![]() 产品15件;
产品15件;
(Ⅲ) ![]() ,
,
∵![]() ,
,
∴![]() 随
随![]() 的增大而减小,
的增大而减小,
∴![]() 时,
时,![]() 有最大值.
有最大值.
y最大=-200×23+44000=39400元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,按以下步骤作图:①分别以A、B为圆心,大于![]() AB的长为半径画弧,两弧相交于点M、N;②作直线MN交AC于点D,连接BD.若CD=CB,∠A=35°,则∠C等于( )
AB的长为半径画弧,两弧相交于点M、N;②作直线MN交AC于点D,连接BD.若CD=CB,∠A=35°,则∠C等于( )

A. 40° B. 50° C. 60° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对中国民族乐器的喜爱情况,某校在全校范围内随机抽取了部分学生进行问卷调查,要求学生在“古筝、二胡、竹笛、扬琴、琵琶”五个选项中,选取自己喜爱的一种乐器(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的两幅不完整的统计图.请你根据图中提供的信息回答下列问题:
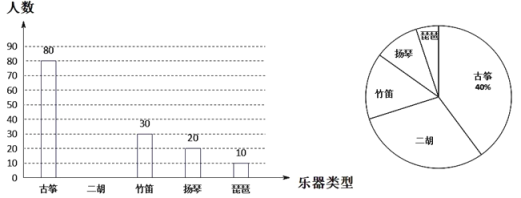
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若该校共有2020名学生,请你估计该校喜爱“竹笛”的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠C=90°,AB=10,点F是AB的中点,点D、E分别在AC、BC边上运动,且始终保持DF⊥EF,则△CDE面积的最大值为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,![]() ,AO是∠BAC的平分线,与AB的垂直平分线DO交于点O,∠ACB沿EF折叠后,点C 刚好与点O重合.下列结论错误的是( )
,AO是∠BAC的平分线,与AB的垂直平分线DO交于点O,∠ACB沿EF折叠后,点C 刚好与点O重合.下列结论错误的是( )
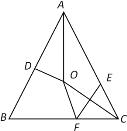
A.AO=COB.∠ECO=∠FCOC.EF⊥OCD.∠BFO=2∠FOC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的图象与
)的图象与![]() 轴交于点
轴交于点![]() 和点
和点![]() (点
(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)用含![]() 的代数式表示点
的代数式表示点![]() 和点
和点![]() 的坐标;
的坐标;
(2)垂直于![]() 轴的直线
轴的直线![]() 在点
在点![]() 与点
与点![]() 之间平行移动,且与抛物线和直线
之间平行移动,且与抛物线和直线![]() 分别交于点
分别交于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() .
.
①当![]() 时,求
时,求![]() 的值;
的值;
②若![]() ,则当
,则当![]() 为何值时,
为何值时,![]() 取得最大值,并求出这个最大值.
取得最大值,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个分别标有数字-1,-2,3,4的小球,它们的形状、大小完全相同.小红先从口袋中随机摸出一个小球记下数字为x;小颖在剩下的3个小球中随机摸出一个小球记下数字为y.
(1)小红摸出标有数字3的小球的概率是________;
(2)请用列表或画树状图的方法表示出由x,y确定的点P(x,y)所有可能的结果;
(3)若规定:点P(x,y)在第一象限或第三象限小红获胜,点P(x,y)在第二象限或第四象限小颖获胜,请分别求出两人获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG.
(1)求证:DF是⊙O的切线;
(2)若AD=DP,OB=3,求![]() 的长度;
的长度;
(3)若DE=4,AE=8,求线段EG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
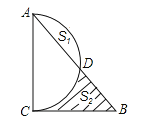
【题目】以△ABC的边AC为直径的半圆交AB边于D点,∠A、∠B、∠C所对边长为a、b、c,且二次函数y=![]() (a+c)x2-bx+
(a+c)x2-bx+![]() (c-a)顶点在x轴上,a是方程z2+z-20=0的根.
(c-a)顶点在x轴上,a是方程z2+z-20=0的根.
(1)证明:∠ACB=90°;
(2)若设b=2x,弓形面积S弓形AED=S1,阴影面积为S2,求(S2-S1)与x的函数关系式;
(3)在(2)的条件下,当BD为何值时,(S2-S1)最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com