
【题目】以△ABC的边AC为直径的半圆交AB边于D点,∠A、∠B、∠C所对边长为a、b、c,且二次函数y=![]() (a+c)x2-bx+
(a+c)x2-bx+![]() (c-a)顶点在x轴上,a是方程z2+z-20=0的根.
(c-a)顶点在x轴上,a是方程z2+z-20=0的根.
(1)证明:∠ACB=90°;
(2)若设b=2x,弓形面积S弓形AED=S1,阴影面积为S2,求(S2-S1)与x的函数关系式;
(3)在(2)的条件下,当BD为何值时,(S2-S1)最大?
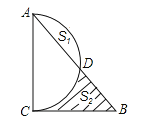
【答案】(1)证明见解析;(2)S2-S1=-![]() x2+4x;(3)BD=
x2+4x;(3)BD=![]() .
.
【解析】
(1)由抛物线的顶点在![]() 轴上,得到
轴上,得到![]() 从而可得结论.
从而可得结论.
(2)利用a是z2+z-20=0的根,求解![]() 的值,再利用S2-S1=S△ABC-(S半圆-S1)-S1=S△ABC-S半圆,从而可得答案,
的值,再利用S2-S1=S△ABC-(S半圆-S1)-S1=S△ABC-S半圆,从而可得答案,
(3)由(2)的函数关系式求解(![]() )最大时
)最大时![]() ,利用直径所对的圆周角是直角,得到
,利用直径所对的圆周角是直角,得到![]() 利用相似三角形的性质可得答案.
利用相似三角形的性质可得答案.
(1)因为二次函数y=![]() (a+c)x2-bx+
(a+c)x2-bx+![]() (c-a)的顶点在x轴上,
(c-a)的顶点在x轴上,
∴ Δ=0,即:b2-4×![]() (a+c)×
(a+c)×![]() (c-a)=0,
(c-a)=0,
∴ c2=a2+b2,
得∠ACB=90°.
(2)∵ z2+z-20=0.
∴ z1=-5,z2=4,
∵ a>0,得a=4.
设b=AC=2x,有S△ABC=![]() AC·BC=4x,S半圆=
AC·BC=4x,S半圆=![]() x2
x2
∴ S2-S1=S△ABC-(S半圆-S1)-S1=S△ABC-S半圆=-![]() x2+4x
x2+4x
(3)![]() S2-S1=-
S2-S1=-(x-
![]() )2+
)2+![]() ,
,
∴ 当x=![]() 时,(S2-S1)有最大值
时,(S2-S1)有最大值![]() .
.
这时,b=![]() ,a=4,c=
,a=4,c=![]() ,
,
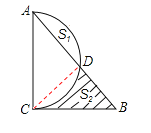
如图,连接![]()
![]() 为圆的直径,
为圆的直径,
![]()
![]()
![]()
![]()
![]() BD=
BD=![]() .
.
当BD为![]() 时,(S2-S1)最大.
时,(S2-S1)最大.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】某公司有甲种原料![]() ,乙种原料
,乙种原料![]() ,计划用这两种原料生产
,计划用这两种原料生产![]() 、
、![]() 两种产品共40件.生产每件
两种产品共40件.生产每件![]() 种产品需甲种原料
种产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,可获利润900元;生产每件
,可获利润900元;生产每件![]() 种产品需甲种原料
种产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,可获利润1100元.设安排生产
,可获利润1100元.设安排生产![]() 种产品
种产品![]() 件(
件(![]() 为非负整数). .
为非负整数). .
(I)根据题意,填写下表:
甲( | 乙( | 件数(件) | |
|
|
| |
|
|
|
(Ⅱ) 安排生产![]() 、
、![]() 两种产品的件数有几种方案?试说明理由:
两种产品的件数有几种方案?试说明理由:
(Ⅲ) 设生产这批40件产品共可获利润![]() 元,将
元,将![]() 表示为
表示为![]() 的函数,并求出最大利润.
的函数,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l:y=kx和抛物线C:y=ax2+bx+1.
(1)当k=1,b=1时,抛物线C:y=ax2+bx+1的顶点在直线l:y=kx上,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点;
(i)求此抛物线的解析式;
(ii)若P是此抛物线上任一点,过点P作PQ∥y轴且与直线y=2交于点Q,O为原点,
求证:OP=PQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在每个边长都为1的小正方形组成的网格中,点![]() 、
、![]() 、
、![]() 均为格点.
均为格点.
(1)线段![]() 的长度等于______;
的长度等于______;
(2)若![]() 为线段
为线段![]() 上的动点,以
上的动点,以![]() 、
、![]() 为邻边的四边形
为邻边的四边形![]() 为平行四边形,当
为平行四边形,当![]() 长度最小时,请你借助网格和无刻度的直尺画出该平行四边形,并简要说明你的作图方法:__________(不要求证明).
长度最小时,请你借助网格和无刻度的直尺画出该平行四边形,并简要说明你的作图方法:__________(不要求证明).
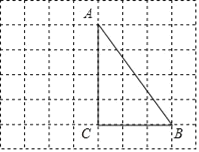
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,O为坐标原点,A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,点
中,点![]() 是边
是边![]() 上一点(不与点
上一点(不与点![]() 重合),点
重合),点![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() ,连接
,连接![]() .
.
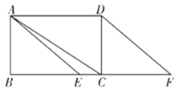
(1)求证:![]()
(2)连接![]() ,其中
,其中![]()
①当四边形![]() 是菱形时,求线段
是菱形时,求线段![]() 与线段
与线段![]() 之间的距离;
之间的距离;
②若点![]() 是
是![]() 的内心,连接
的内心,连接![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
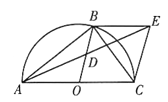
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 上一点,且点
上一点,且点![]() 不与点
不与点![]() 重合,点
重合,点![]() 为半径
为半径![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
(1)求证:点![]() 为
为![]() 的中点;
的中点;
(2)连接![]() ,若
,若![]() ,请直接写出
,请直接写出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某电暖科技有限公司准备购进A型(直热式电暖)和B型(智能电风幕电暖)两种设备,经计算,购进 3 台A设备和 2 台B设备需用 6.6 万元,购进 1 台A设备和 3 台B设备需用5. 7 万元 .
请解答下列问题:
(1)求A、B两种设备的进价;
(2)该公司计划用 21 万元同时购进A、B两种设备,若A设备以每台1.5万元的价格出售,B设备以每台2万元的价格出售,且全部售出,请求出所获利润W(单位:万元)与购买A设备的资金m(单位:万元)之间的函数关系式;
(3)在(2)的条件下,要求A设备的利润不低于B设备的利润,并将(2)中的最大利润全部用于购买甲(小米笔记本4000元/台)、乙(华为笔记本6000元/台)两种型号的电脑赠给某中学,请求出有几种购买电脑的方案 .
查看答案和解析>>
科目:初中数学 来源: 题型:
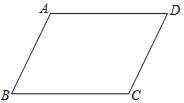
【题目】如图,已知四边形ABCD是平行四边形,AB<AD.
(1)利用尺规作图作出∠ABC的角平分线BG,交AD于点E,记点A关于BE对称点为F(要求保留作图痕迹,不写作法);
(2)在(1)所作的图中,若AF=6,AB=5,求BE的长和四边形ABFE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com