
【题目】如图,在矩形![]() 中,点
中,点![]() 是边
是边![]() 上一点(不与点
上一点(不与点![]() 重合),点
重合),点![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() ,连接
,连接![]() .
.
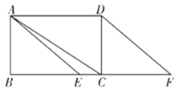
(1)求证:![]()
(2)连接![]() ,其中
,其中![]()
①当四边形![]() 是菱形时,求线段
是菱形时,求线段![]() 与线段
与线段![]() 之间的距离;
之间的距离;
②若点![]() 是
是![]() 的内心,连接
的内心,连接![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)①线段![]() 与线段
与线段![]() 之间的距离为
之间的距离为![]() ,②
,②![]() .
.
【解析】
(1)根据已知,利用SAS即可证明;
(2)①因为四边形![]() 是菱形,所以AE与DF的距离等于AD与EF之间的距离,即CD为所求,再利用勾股定理即可求解;
是菱形,所以AE与DF的距离等于AD与EF之间的距离,即CD为所求,再利用勾股定理即可求解;
②如图作出辅助线,根据△ABE![]() △DCF(SAS),
△DCF(SAS),![]() 的取值范围即可转化为在△ABE中进行求解,找到E点在B、C两点临界处的∠AED的取值范围,利用三角形内角和=180
的取值范围即可转化为在△ABE中进行求解,找到E点在B、C两点临界处的∠AED的取值范围,利用三角形内角和=180![]() ,即可求得.
,即可求得.
(1)证明:∵四边形ABCD是矩形,
∴AB=DC, ∠B=∠BCD=90![]() ,
,
∴∠B=∠DCF=90![]() ,
,
∵BE=CF,
∴△ABE![]() △DCF(SAS).
△DCF(SAS).
(2)解:①∵四边形AEFD是菱形,
∴ AE与DF的距离等于AD与EF之间的距离,即CD的长,
∵AC=![]() ,BC=AD=6,在△ADC中,
,BC=AD=6,在△ADC中,
∴![]() ,
,
∴线段AE与线段DF之间的距离为![]() .
.
②∵△ABE![]() △DCF,
△DCF,
∴△DCF的内心即为△ABE的内心,
如图:作出∠AEB、∠ABE的角平分线BQ、EQ,
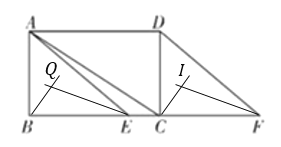
则∠BQE=∠CIF, ∠BQE即为所求,
∵∠ABE恒等于90![]() ,
,
∴![]() ∠ABE恒等于45
∠ABE恒等于45![]() ,
,
∵当点E在点B处时,∠AEB=90![]() ,
,
当点E在点C处时,在Rt△ABE 中,AB=![]() AC,知∠AEB=30
AC,知∠AEB=30![]() ,
,
∴所以30![]() ∠AEB
∠AEB![]() ,
,
∴15![]() ∠AEB
∠AEB![]() ,
,
∴ ![]() ∠ABE+
∠ABE+![]() ∠AEB
∠AEB![]() ,
,
即![]() ∠ABE+
∠ABE+![]() ∠AEB
∠AEB![]() ,
,
而∠BQE=180![]() -
-![]() ∠ABE+
∠ABE+![]() ∠AEB,
∠AEB,
∴![]() ∠BQE
∠BQE![]() ,
,
即![]() ∠BQE
∠BQE![]() .
.
即![]() ∠CIF
∠CIF![]() .
.
故 90![]() ∠CIF
∠CIF![]() .
.


科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的图象与
)的图象与![]() 轴交于点
轴交于点![]() 和点
和点![]() (点
(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)用含![]() 的代数式表示点
的代数式表示点![]() 和点
和点![]() 的坐标;
的坐标;
(2)垂直于![]() 轴的直线
轴的直线![]() 在点
在点![]() 与点
与点![]() 之间平行移动,且与抛物线和直线
之间平行移动,且与抛物线和直线![]() 分别交于点
分别交于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() .
.
①当![]() 时,求
时,求![]() 的值;
的值;
②若![]() ,则当
,则当![]() 为何值时,
为何值时,![]() 取得最大值,并求出这个最大值.
取得最大值,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和爸爸周末步行去游泳馆游泳,爸爸先出发了一段时间后小明才出发,途中小明在离家![]() 米处的报亭休息了一段时间后继续按原来的速度前往游泳馆.爸爸、小明离家的距离
米处的报亭休息了一段时间后继续按原来的速度前往游泳馆.爸爸、小明离家的距离![]() (单位:米),
(单位:米),![]() 单位:米)与小明所走时间
单位:米)与小明所走时间![]() (单位:分钟)之间的函数关系如图所示,请结合图象信息解答下列问题:
(单位:分钟)之间的函数关系如图所示,请结合图象信息解答下列问题:

![]() 分别求出爸爸离家的距离
分别求出爸爸离家的距离![]() 和小明到达报亭前离家的距离
和小明到达报亭前离家的距离![]() 与时间
与时间![]() 之间的函数关系式;
之间的函数关系式;
![]() 求小明在报亭休息了多长时间遇到姗姗来迟的爸爸?
求小明在报亭休息了多长时间遇到姗姗来迟的爸爸?
![]() 若游泳馆离小明家
若游泳馆离小明家![]() 米,请你通过计算说明谁先到达游泳馆?
米,请你通过计算说明谁先到达游泳馆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:
第一步:对折矩形纸片![]() ,使
,使![]() 与
与![]() 重合,得到折痕
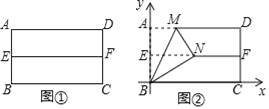
重合,得到折痕![]() ,把纸片展开(如图①);
,把纸片展开(如图①);
第二步:再一次折叠纸片,使点![]() 落在
落在![]() 上,并使折痕经过点
上,并使折痕经过点![]() ,得到折痕
,得到折痕![]() ,同时得到线段
,同时得到线段![]() (如图②).
(如图②).
如图②所示建立平面直角坐标系,请解答以下问题:
(Ⅰ)设直线![]() 的解析式为
的解析式为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若![]() 的延长线与矩形
的延长线与矩形![]() 的边
的边![]() 交于点
交于点![]() ,设矩形的边
,设矩形的边![]() ,
,![]() ;
;
(i)若![]() ,
,![]() ,求
,求![]() 点的坐标;
点的坐标;
(ii)请直接写出![]() 、
、![]() 应该满足的条件.
应该满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
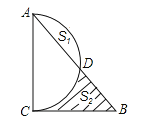
【题目】以△ABC的边AC为直径的半圆交AB边于D点,∠A、∠B、∠C所对边长为a、b、c,且二次函数y=![]() (a+c)x2-bx+
(a+c)x2-bx+![]() (c-a)顶点在x轴上,a是方程z2+z-20=0的根.
(c-a)顶点在x轴上,a是方程z2+z-20=0的根.
(1)证明:∠ACB=90°;
(2)若设b=2x,弓形面积S弓形AED=S1,阴影面积为S2,求(S2-S1)与x的函数关系式;
(3)在(2)的条件下,当BD为何值时,(S2-S1)最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
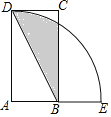
【题目】如图,四边形ABCD为矩形,以A为圆心,AD为半径的弧交AB的延长线于点E,连接BD,若AD=2AB=4,则图中阴影部分的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
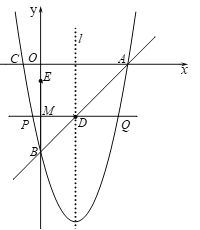
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,抛物线的对称轴
,抛物线的对称轴![]() 交
交![]() 于点
于点![]() .
.
(1)求抛物线的函数关系式及对称轴;
(2)若![]() 为
为![]() 轴上一动点,
轴上一动点,![]() 为
为![]() 的中点,过点
的中点,过点![]() 作
作![]() 的中垂线,交抛物线于点
的中垂线,交抛物线于点![]() ,其中
,其中![]() 在
在![]() 的左边.
的左边.
①如图1,若![]() 时,求
时,求![]() 的长.
的长.
②当以点![]() 为顶点的三角形是直角三角形时,请直接写出点
为顶点的三角形是直角三角形时,请直接写出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
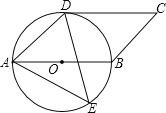
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
(1)试判断CD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为3,sin∠ADE=![]() ,求AE的值.
,求AE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com