练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，中，对角线与相交于点点为的中点，连接的延长线交的延长线于点连接．

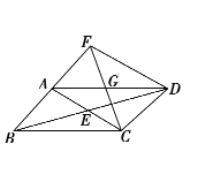
    （1）求证：；

    （2）若判断四边形的形状，并证明你的结论．

    【答案】（1）见解析；（2）四边形是矩形，理由见解析．

    【解析】

    （1）先根据平行四边形的性质和平行线的性质得出，然后利用ASA即可证明；

    （2）首先根据全等三角形的性质得出，进而可证四边形是平行四边形，然后利用平行四边形的性质和角度之间的关系得出是等边三角形，则有，进而得出，最后利用对角线相等的平行四边形是矩形即可证明．

    证明:四边形是平行四边形，

    ，

    ．

    点是的中点，

    ．

    又，

    ；

    解:四边形是矩形.

    理由:,

    ，．

    又，

    四边形是平行四边形．

    四边形是平行四边形，

    ，

    ．

    又，

    ．

    ，

    ，

    是等边三角形，

    ．

    ，

    ，

    四边形是矩形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知在△ABC中，AB=AC，∠BAC=α，直线l经过点A（不经过点B或点C），点C关于直线l的对称点为点D，连接BD，CD．

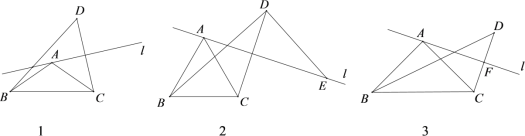
    （1）如图1，

    ①求证：点B，C，D在以点A为圆心，AB为半径的圆上；

    ②直接写出∠BDC的度数（用含α的式子表示）为 ；

    （2）如图2，当α=60°时，过点D作BD的垂线与直线l交于点E，求证：AE=BD；

    （3）如图3，当α=90°时，记直线l与CD的交点为F，连接BF．将直线l绕点A旋转的过程中，在什么情况下线段BF的长取得最大值？若AC=2a，试写出此时BF的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形中，点是边上一点(不与点重合)，点是延长线上一点，且，连接．

    （1）求证：

    （2）连接，其中

    ①当四边形是菱形时,求线段与线段之间的距离；

    ②若点是的内心，连接，直接写出的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，菱形 的对角线交于点 是线段上一动点， E 是线段 AB上一个动点，则 的最小值为 ____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市某电暖科技有限公司准备购进A型（直热式电暖）和B型（智能电风幕电暖）两种设备，经计算，购进 3 台A设备和 2 台B设备需用 6.6 万元，购进 1 台A设备和 3 台B设备需用5. 7 万元 ．

    请解答下列问题：

    （1）求A、B两种设备的进价；

    （2）该公司计划用 21 万元同时购进A、B两种设备，若A设备以每台1.5万元的价格出售，B设备以每台2万元的价格出售，且全部售出，请求出所获利润W（单位：万元）与购买A设备的资金m（单位：万元）之间的函数关系式；

    （3）在（2）的条件下，要求A设备的利润不低于B设备的利润，并将（2）中的最大利润全部用于购买甲（小米笔记本4000元/台）、乙（华为笔记本6000元/台）两种型号的电脑赠给某中学，请求出有几种购买电脑的方案 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

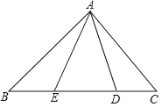
    【题目】如图，在Rt△ABC中，AB＝AC，D、E是斜边BC上的两点，且∠DAE＝45°．设BE＝a，DC＝b，那么AB＝_____（用含a、b的式子表示AB）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

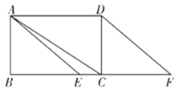
    【题目】如图，DB∥AC，且DB=AC，E是AC的中点．

    （1）求证：四边形BDEC是平行四边形；

    （2）连接AD、BE，△ABC添加一个条件： ，使四边形DBEA是矩形（不需说明理由）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图1、图2均是的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为1，点、、、均在格点上．在图1、图2中，只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上，不要求写出画法．

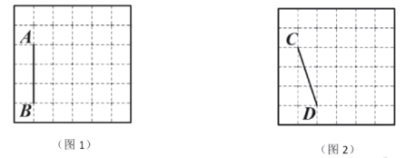
    （1）在图1中以线段为边画一个，使，且的面积为3；

    （2）在图2中以线段为边画一个四边形，使四边形既是轴对称图形又是中心对称图形；

    （3）直接写出四边形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

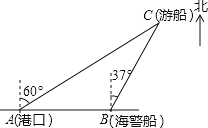
    【题目】 一艘观光游船从港口A以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以40海里每小时的速度前往救援，求海警船到大事故船C处所需的大约时间．（温馨提示：sin53°≈0.8，cos53°≈0.6）

    查看答案和解析>>

    同步练习册答案