练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，DB∥AC，且DB=AC，E是AC的中点．

    （1）求证：四边形BDEC是平行四边形；

    （2）连接AD、BE，△ABC添加一个条件： ，使四边形DBEA是矩形（不需说明理由）．

    【答案】（1）见解析；（2）AB=BC.

    【解析】

    （1）证明DB=EC． DB∥EC即可；

    （2）矩形的判定方法有多种，可选择利用“对角线相等的平行四边形为矩形”来解决．

    （1）证明：∵E是AC中点，

    ∴EC=AC．

    ∵DB=AC，

    ∴DB=EC．

    又∵DB∥EC，

    ∴四边形DBCE是平行四边形．

    （2）如图，连接AD，BE，

    添加AB=BC．

    理由：∵DB∥AE，DB=AE，

    ∴四边形DBEA是平行四边形．

    ∵BC=DE，AB=BC，

    ∴AB=DE．

    ∴ADBE是矩形．

    故答案为：AB=BC．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校为奖励学习之星，准备在某商店购买A、B两种文具作为奖品，已知一件A种文具的价格比一件B种文具的价格便宜5元，且用600元买A种文具的件数是用400元买B种文具的件数的2倍．

    （1）求一件A种文具的价格；

    （2）根据需要，该校准备在该商店购买A、B两种文具共150件．

    ①求购买A、B两种文具所需经费W与购买A种文具的件数a之间的函数关系式；

    ②若购买A种文具的件数不多于B种文具件数的2倍，且计划经费不超过2750元，求有几种购买方案，并找出经费最少的方案，及最少需要多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）已知：点A和点B（如图1），根据条件画图（用三角板和量角器）：

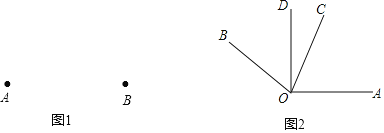
    ①画射线BA；

    ②画∠ABC＝90°，使得点C在线段AB上方且AB＝BC；

    ③连接AC，画出∠ABC的角平分线BD，交AC于D．通过观察、度量、猜想获得线段BD、AC的关系．

    （2）已知：如图2，∠AOB＝150，OC平分∠AOB，AO⊥DO，求∠COD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将口ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F．

    （1）求证：△ABF≌△ECF

    （2）若∠AFC=2∠D，连接AC、BE．求证：四边形ABEC是矩形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在梯形ABCD中，∠ABC=90°，AD∥BC，AE∥CD交BC于E，∠BAE=∠EAC，O是AC的中点，AD=DC=2，下面结论：①AC=2AB；②AB=；③S△ADC=2S△ABE；④BO⊥AE，其中正确的个数是（　　）

    A. 1B. 2C. 3D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，过点A（0，3）的一次函数y1=kx+b（k≠0）的图象与正比例函数y2=2x的图象相交于点B，且点B的横坐标是1．

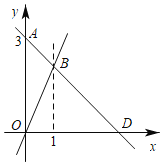
    （1）求点B的坐标及k、b的值；

    （2）若该一次函数的图象与x轴交于D点，求△BOD的面积

    （3）当y1≤y2时，自变量x的取值范围为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD为平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E．

    （1）求证：BE=CD；

    （2）连接BF，若BF⊥AE，∠BEA=60°，AB=4，求平行四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知平面直角坐标系（如图），直线的经过点和点.

    （1）求、的值；

    （2）如果抛物线经过点、，该抛物线的顶点为点，求的值；

    （3）设点在直线上，且在第一象限内，直线与轴的交点为点，如果，求点的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，矩形OABC的顶点A在y轴的正半轴上，点C在x轴的正半轴上，线段OA,OC的长分别是m，n且满足(m-6)2+＝0，点D是线段OC上一点，将△AOD沿直线AD翻折，点O落在矩形对角线AC上的点E处

    （1）求线段OD的长

    （2）求点E的坐标

    （3）DE所在直线与AB相交于点M，点N在x轴的正半轴上，以M、A、N、C为顶点的四边形是平行四边形时，求N点坐

    查看答案和解析>>

    同步练习册答案